题目内容
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且sinA+
cosA=2．
（Ⅰ）求角A的大小；
（Ⅱ）现给出三个条件：①a=2；②B=45°；③c= 
．试从中选出两个可以确△ABC的条件，写出你的选择，并以此为依据求△ABC的面积．（只写出一个方案即可）
【答案】（Ⅰ）
（Ⅱ） 选择①②, 
【解答】解：（Ⅰ）依题意得2sin（A+
）=2，即sin（A+）=1，
∵0＜A＜π，
∴＜A+
＜
，
∴A+=
，
∴A=
．
（Ⅱ）选择①②由正弦定理
=
，得b=
sinB=2
，
∵A+B+C=π，
∴sinC=sin（A+B）=sinAcosB+cosAsinB=
+
，
∴S=
absinC=×2×2×
=
+1．
【解析】试题分析：（1）根据题目条件，利用辅助角公式，再结合
是三角形的内角，即可求出
的大小；（2）根据（1）的结论，利用条件①
， ②
，并结合正弦定理，即可求出
边，进而可求出
边和角
，从而可确定
,并可以求得其面积.
试题解析：（1）由
，得
因为
，所以
，
所以
，即
（2）方案一：选①和②
由正弦定理得， 
又， 
的面积为
方案二：选①和③
由余弦定理得， 
则
，
解得
，于是
的面积为
愉快的寒假南京出版社系列答案
【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入4万元广告费，并将各地的销售收益绘制成频率分布直方图（如图所示），由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的．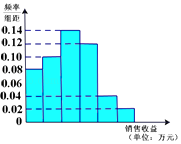 
（1）根据频率分布直方图计算各小长方形的宽度；
（2）估计该公司投入4万元广告费之后，对应销售收益的平均值（以各组的区间中点值代表该组的取值）
（3）该公司按照类似的研究方法，测得另外一些数据，并整理得到下表：
广告投入x（单位：万元） | 1 | 2 | 3 | 4 | 5 |
销售收益y（单位：万元） | 2 | 3 | 2 | 7 |
表格中的数据显示，x与y之间存在线性相关关系，请将（2）的结果填入空白栏，并计算y关于x的回归方程．
回归直线的斜率和截距的最小二乘法估计公式分别为 
， 
．
【题目】某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现，但生猪养殖成本逐月递增．下表是今年前四个月的统计情况：
月份 | 1月份 | 2月份 | 3月份 | 4月份 |
收购价格（元/斤） | 6 | 7 | 6 | 5 |
养殖成本（元/斤） | 3 | 4 | 4.6 | 5 |
现打算从以下两个函数模型：
①y=Asin（ωx+φ）+B，（A＞0，ω＞0，﹣π＜φ＜π），
②y=log2（x+a）+b
中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．
（1）请你选择适当的函数模型，分别求出这两个函数解析式；
（2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在8月和9月有没有可能亏损？