题目内容
已知椭圆 经过点
经过点 ,离心率
,离心率 ,直线
,直线 与椭圆交于
与椭圆交于 ,
, 两点,向量
两点,向量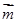
 ,
,
 ,且
,且 .
.
(1)求椭圆的方程;
(2)当直线 过椭圆的焦点
过椭圆的焦点 (
( 为半焦距)时,求直线
为半焦距)时,求直线 的斜率
的斜率 .
.
(1)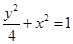 (2)
(2)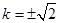
解析试题分析:(1)将点 代入椭圆方程,并与
代入椭圆方程,并与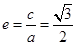 和
和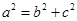 联立,解方程组可得
联立,解方程组可得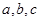 的值。(2)由(1)知
的值。(2)由(1)知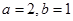 ,
,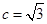 ,则
,则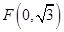 ,
,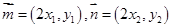 。则可设
。则可设 的方程为
的方程为 ,与椭圆方程联立消去
,与椭圆方程联立消去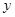 整理为关于
整理为关于 的一元二次方程,可得根与系数的关系。因为
的一元二次方程,可得根与系数的关系。因为 所以
所以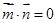 ,根据数量积公式可得
,根据数量积公式可得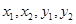 的关系式,将所得的根与系数的关系代入上式可求得
的关系式,将所得的根与系数的关系代入上式可求得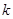 。
。
(1)∵ ∴
∴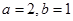
∴椭圆的方程为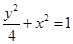 (5分)
(5分)
(2)依题意,设 的方程为
的方程为 ,
,
由  显然
显然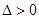 ,(8分)
,(8分) , 由已知
, 由已知
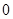 得:
得: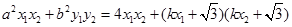
 (12分)
(12分)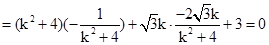 ,解得
,解得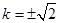
考点:1椭圆的简单几何性质;2直线与椭圆的位置关系。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
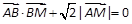 ,
, 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且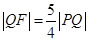 .
.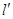 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程. 中,点
中,点 到点
到点 的距离比它到
的距离比它到 轴的距离多1,记点
轴的距离多1,记点 .
. 的直线
的直线 过定点
过定点 ,求直线
,求直线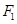 ,
,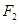 分别是椭圆
分别是椭圆 :
: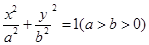 的左、右焦点,过点
的左、右焦点,过点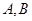 两点,
两点,
 的周长为16,求
的周长为16,求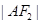 ;
;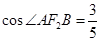 ,求椭圆
,求椭圆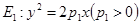 和
和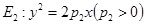 ,过原点
,过原点 的两条直线
的两条直线 和
和 ,
, 分别交于
分别交于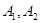 两点,
两点,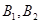 两点.
两点.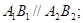
 (异于
(异于 两点.记
两点.记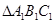 与
与 的面积分别为
的面积分别为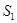 与
与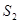 ,求
,求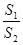 的值.
的值.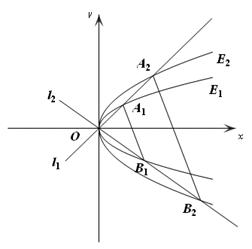
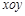 中,已知椭圆的焦点在
中,已知椭圆的焦点在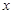 轴上,离心率为
轴上,离心率为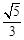 ,且经过点
,且经过点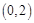 .
. ,设
,设 为圆
为圆 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点, 为
为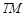 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点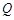 .问:直线
.问:直线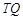 能否与圆
能否与圆 ,一条准线的方程为x=2
,一条准线的方程为x=2 .
.
 ,其中M,N是椭圆上的点.直线OM与ON的斜率之积为﹣
,其中M,N是椭圆上的点.直线OM与ON的斜率之积为﹣ .
.