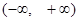题目内容
已知函数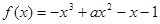 在
在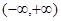 上是单调函数,则实数
上是单调函数,则实数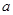 的取值范围是( )
的取值范围是( )
A.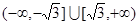 | B.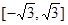 |
C.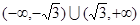 | D.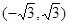 |
B
解析试题分析:由f(x)的解析式求出导函数,导函数为开口向下的抛物线,因为函数在R上为单调函数,所以导函数与x轴没有交点,即△小于等于0,列出关于a的不等式,求出不等式的解集即可得到实数a的取值范围.解:由f(x)=-x3+ax2-x-1,得到f′(x)=-3x2+2ax-1,因为函数在(-∞,+∞)上是单调函数,所以f′(x)=-3x2+2ax-1≤0在(-∞,+∞)恒成立,则△=4a2-12≤0⇒-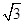 ≤a≤
≤a≤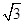 ,所以实数a的取值范围是:[-
,所以实数a的取值范围是:[-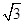 ,
,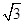 ].故选B
].故选B
考点:导函数的正负确定函数的单调区间
点评:此题考查学生会利用导函数的正负确定函数的单调区间,掌握函数恒成立时所取的条件,是一道综合题.

练习册系列答案
相关题目
已知函数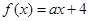 ,若
,若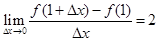 ,则实数
,则实数 的值为( )
的值为( )
A.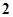 | B.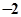 | C.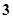 | D.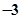 |
已知点 在曲线
在曲线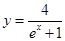 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 的取值范围为( )
的取值范围为( )
A.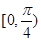 | B.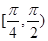 | C. | D.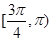 |
已知函数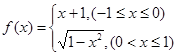 , 则
, 则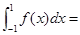 ( )
( )
A. | B.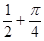 | C.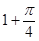 | D.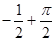 |
若函数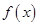 在R 上可导,且满足
在R 上可导,且满足 ,则( )
,则( )
A.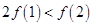 | B.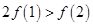 | C.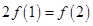 | D.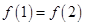 |
已知函数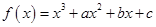 ,若
,若 在区间
在区间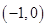 上单调递减,则
上单调递减,则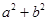 的取值范围是C
的取值范围是C
A.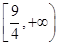 | B.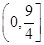 | C.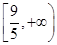 | D.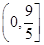 |
函数 =
=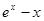 (
(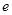
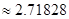 )在区间[-1,1]上的最大值是( )
)在区间[-1,1]上的最大值是( )
A.1+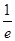 | B.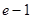 | C.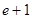 | D.1 |
若函数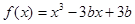 在
在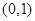 内有极小值,则 ( )
内有极小值,则 ( )
A.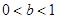 | B.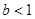 | C.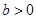 | D.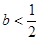 |
 为曲线
为曲线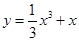 上的任意一点,在点
上的任意一点,在点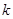 ,则
,则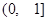 B
B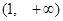 C.
C.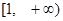 D.
D.