题目内容
已知函数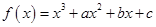
，若
在区间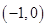
上单调递减，则
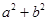的取值范围是C
A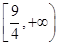． | B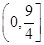． | C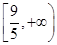． | D． |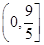
B
解析试题分析：根据题意，由于函数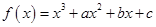，若在区间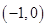上单调递减，则说明导数
在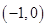上恒成立，则根据不等式恒成立，结合二次方程根的分布问题可知，
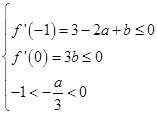，那么可知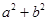表示的 为区域内的点到原点距离平方的取值范围，那么结合线性区域可知，过点（0，
）时，距离最大，则距离的平方为
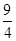，因此答案为B
考点：函数单调性
点评：解决函数在区间上的单调性已知求参数的范围的问题，递增时令导函数大于等于0恒成立；递减时，令导数小于等于0恒成立．
练习册系列答案
名校课堂系列答案
相关题目
设
，若函数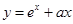
，
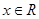，有大于零的极值点，则（ ）
A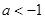． | B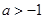． | C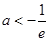． | D． |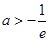
函数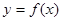
在一点的导数值为
是函数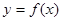在这点取极值的( )
| A．充分条件 | B．必要条件 | C．必要非充分条件 | D．充要条件 |
已知函数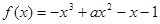
在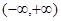
上是单调函数,则实数
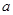的取值范围是( )
A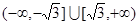． | B． |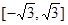
C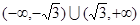． | D． |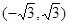
若
，则
等于
| A．2 | B．－2 | C． | D． |
已知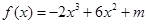
（
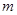为常数）在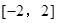
上有最小值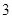
，那么此函数在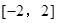上的最大值为( )
A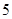． | B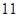． | C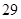． | D． |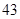
曲线
上的点到直线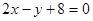
的最短距离是（ ）
A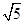． | B． | C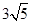． | D．0 |
已知函数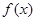
在
上连续可导，则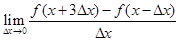
等于 （ ）
A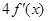． | B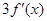． | C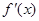． | D． |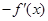
设
为曲线
：
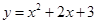上的点，且曲线在点处切线倾斜角的取值范围为
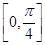，则点横坐标的取值范围为 ( )
A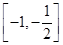． | B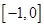． | C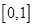． | D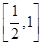． |