题目内容
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C的离心率为![]() ,且椭圆C过点
,且椭圆C过点![]() .
.
(1)求椭圆C的标准方程:
(2)若直线l:![]() 与椭圆C相交于A,B两点(A,B不是左右顶点),且以
与椭圆C相交于A,B两点(A,B不是左右顶点),且以![]() 为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
【答案】(1)![]() (2)证明见解析;定点坐标为
(2)证明见解析;定点坐标为![]()
【解析】
(1) 由题意结合离心率首先确定![]() 的关系,然后结合椭圆经过的点即可确定椭圆方程;
的关系,然后结合椭圆经过的点即可确定椭圆方程;
(2) 把直线![]() 的方程与椭圆的方程联立可得根与系数的关系,再利用以
的方程与椭圆的方程联立可得根与系数的关系,再利用以![]() 为直径的圆过椭圆的右顶点D,可得
为直径的圆过椭圆的右顶点D,可得![]() ,即可得出
,即可得出![]() 与
与![]() 的关系,从而得出答案.
的关系,从而得出答案.
解:(1)由题意设椭圆的标准方程为![]() (
(![]() ),
),![]() ,椭圆C过点
,椭圆C过点![]() ,
,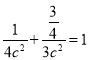 ,解得
,解得![]()
∴椭圆的标准方程为![]() .
.
(2)设![]() ,
,![]() ,直线
,直线![]() 代入椭圆方程得
代入椭圆方程得
得![]() ,
,
![]() ,即
,即![]() ,则
,则
![]() ,
,![]() .
.
又![]() ,
,
因为以![]() 为直径的圆过椭圆的右焦点
为直径的圆过椭圆的右焦点![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴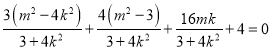 ,∴
,∴![]() .
.
解得![]() ,
,![]() ,且均满足
,且均满足![]() ,
,
当![]() 时,l的方程为
时,l的方程为![]() ,直线过定点
,直线过定点![]() ,与已知矛盾;
,与已知矛盾;
当![]() 时,l的方程为
时,l的方程为![]() ,直线过定点
,直线过定点![]() .
.
所以,直线l过定点,定点坐标为![]() .
.

练习册系列答案
相关题目
【题目】已知函数![]() ,若给定非零实数
,若给定非零实数![]() ,对于任意实数
,对于任意实数![]() ,总存在非零常数
,总存在非零常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 是
是![]() 上的
上的![]() 级
级![]() 类周期函数,若函数
类周期函数,若函数![]() 是
是![]() 上的2级2类周期函数,且当
上的2级2类周期函数,且当![]() 时,
时,![]() ,又函数
,又函数![]() .若
.若![]() ,
,![]() ,使
,使![]() 成立,则实数
成立,则实数![]() 的取值范围是_______.
的取值范围是_______.
【题目】某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |