��Ŀ����
����Ŀ��ij��λ����A��B���ֲ�Ʒ����Ҫ�ʽ�ͳ��أ�����ÿ��A�ֲ�Ʒ������ÿ��B�ֲ�Ʒ�����ʽ�ͳ��ص����������ʾ��
��Դ | �ʽ���Ԫ�� | ���أ�ƽ���ף� |
A | 2 | 100 |
B | 35 | 50 |
�����ʽ�12��Ԫ������400ƽ���ף�����ÿ��A�ֲ�Ʒ�ɻ�����3��Ԫ������ÿ��B�ֲ�Ʒ�ɻ�����2��Ԫ���ֱ���x��y��ʾ�ƻ�����A��B���ֲ�Ʒ�Ķ�����
��1����x��y�г�����������������ѧ��ϵʽ����������Ӧ��ƽ������
��2����A��B���ֲ�ƷӦ���������ٶ֣����ܲ�����������������������
���𰸡�
��1���⣺����֪��x��y�������ѧ��ϵʽΪ�� 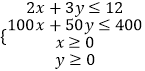 ��
�� 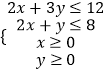
�ö�Ԫһ�β���ʽ������ʾ��ƽ������Ϊ��ͼ����Ӱ���֣�
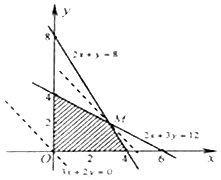
��2���⣺������Ϊz��Ԫ����Ŀ�꺯��Ϊz=3x+2y��
�������Ϊ ![]() ������б��Ϊ
������б��Ϊ ![]() ����z�仯��һ��ƽ��ֱ�ߣ�
����z�仯��һ��ƽ��ֱ�ߣ� ![]() Ϊֱ����y���ϵĽؾ࣬��
Ϊֱ����y���ϵĽؾ࣬�� ![]() ȡ���ֵʱ��z��ֵ���
ȡ���ֵʱ��z��ֵ���
��Ϊx��y����Լ��������
���Ե�ֱ��z=3x+2y�����������ϵĵ�Mʱ���ؾ� ![]() ���z���
���z���
�ⷽ���� ![]() �õ�M�����꣨3��2����
�õ�M�����꣨3��2����
��zmax=3��3+2��2=13��
������A�ֲ�Ʒ3�֡�B�ֲ�Ʒ2��ʱ���������Ϊ13��Ԫ��
����������1��������֪����ֱ���г�����������������ѧ��ϵʽ����������Ӧ��ƽ������2��д��Ŀ�꺯�����������Թ滮��֪ʶ�����Ŀ�꺯������ֵ���ɣ�

 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
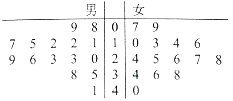
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�����Ŀ��ij�Ա��꾭���Դ���������ڵ������߽���ͳ�ƣ������ڽ�����1000Ԫ������������Ů����Ϊ![]() ���õ갴�˱�����ȡ��100�������߽��н�һ���������õ��±�Ů�����������
���õ갴�˱�����ȡ��100�������߽��н�һ���������õ��±�Ů�����������
���ѽ��(Ԫ) |
|
|
|
|
|
���� | 5 | 10 | 15 | 47 | 3 |
�������������
���ѽ��(Ԫ) |
|
|
|
|
|
���� | 2 | 3 | 10 | 3 | 2 |
�����ѽ�����600Ԫ��������Ϊ���������ˡ�������600Ԫ��������Ϊ�����������ˡ�
(1)�ֱ����Ů�Ժ��������ѵ�ƽ���������ж�ƽ������ˮƽ�ߵ�һ�����������ˡ������Ƿ�����£�
(2)��������ͳ��������д����![]() �����������ش��ܷ��ڷ�����ĸ��ʲ�����
�����������ش��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ���Ƿ�Ϊ���������ˡ����Ա��йء�.
��ǰ������Ϊ���Ƿ�Ϊ���������ˡ����Ա��йء�.
Ů�� | ���� | �ϼ� | |
���������ˡ� | |||
�����������ˡ� | |||
�ϼ� |
����  .
.
|
|
|
|
|
|
|
|
|
|
|
|