题目内容
2．两条异面直线在同一平面内的射影不可能是（ ）| A． | 两条相交直线 | |
| B． | 两条平行直线 | |
| C． | 一条直线和不在这条直线上的一个点 | |
| D． | 两个点 |
分析 根据异面直线的定义，分别分析投影面与已知的两条异面直线及异面直线的公垂线之间的关系，排除可能出现的情况，可得答案．
解答 解：如果投影面与两条异面直线的公垂线垂直，此时两条异面直线的投影为两条相交直线，故不选A；
如果投影面与两条异面直线的公垂线平行，且两条异面直线与投影面均不垂直，此时两条异面直线的投影为两条平行线，故不选B；
如果投影面与两条异面直线的公垂线平行，且有一条直线与投影面垂直，此时两条异面直线的投影为一点和一条直线，故不选C；
但两条异面直线在同一平面的射影不可能是两个点，
故选：D．
点评 本题考查的知识点是空间中直线与直线之间的位置关系，熟练掌握空间异面直线的几何特征是解答的关键．
练习册系列答案
相关题目
2．函数y=ln（2x+5）的导函数f′（x）=（ ）
| A． | $\frac{1}{2x+5}$ | B． | $\frac{2}{2x+5}$ | C． | $\frac{5}{2x+5}$ | D． | $\frac{ln2}{2x+5}$ |
10．执行如图所示的程序框图，若输出的值为-105，则输入的n的值可能是（ ）
| A． | 5 | B． | 7 | C． | 8 | D． | 10 |
7．
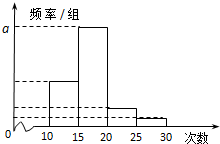公司随机抽取M名员工作为样本，得到这M名员工参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
（Ⅰ）求出表中M和图中a的值；
（Ⅱ）若该公司员工有240人，试估计员工参加社区服务的次数在区间[10，15）内的人数；
（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的员工中任选2人，求至多一人参加社区服务次数在区间[25，30）内的概率．
公司随机抽取M名员工作为样本，得到这M名员工参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：（Ⅰ）求出表中M和图中a的值；
（Ⅱ）若该公司员工有240人，试估计员工参加社区服务的次数在区间[10，15）内的人数；
（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的员工中任选2人，求至多一人参加社区服务次数在区间[25，30）内的概率．
| 分组 | 频数 | 频率 |
| [10，15） | 10 | 0.25 |
| [15，20） | 24 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.05 |
| 合计 | M | 1 |
14．使平面α∥平面β的一个条件是（ ）
| A． | 存在一条直线a，a∥α，a∥β | |
| B． | 存在一条直线a，a?α，a∥β | |
| C． | 存在两条平行直线a、b，a?α，b?β，a∥β，b∥α | |
| D． | 存在两条异面直线a、b，a?α，b?β，a∥β，b∥α |
12．已知i是虚数单位．若复数z满足（1-i）•z=2i3，则复数z=（ ）
| A． | 1+i | B． | 1-i | C． | -1+i | D． | -1-i |