题目内容
13. 已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=EB=BC=2,点F为CE上一点,且BF⊥平面ACE.
已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=EB=BC=2,点F为CE上一点,且BF⊥平面ACE.(1)求证:AE∥平面BFD;
(2)求二面角C-DE-A的余弦值.
分析 (1)证明:连接AC交BD于G,连结GF,证明BF⊥CE,推出FG∥AE然后证明AE∥平面BFD.
(2)取DE中点H,连结AH,CH,说明∠CHA即为二面角C-DE-A的平面角;在△CHA中,求解二面角C-DE-A的余弦值即可.
解答 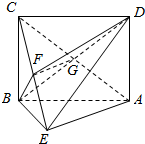 解:(1)证明:连接AC交BD于G,连结GF,∵ABCD是矩形.
解:(1)证明:连接AC交BD于G,连结GF,∵ABCD是矩形.
∴G为AC的中点…1分.
由BF⊥平面ACE得:BF⊥CE,
由EB=BC知:点F为CE中点…2分
∴FG为△ACE的中位线,
∴FG∥AE…3分,
∵AE?平面BFD;FG?平面BFD;
∴AE∥平面BFD;…4分.
(2)由BF⊥平面ACE得:BF⊥AE;
由BC⊥平面ABE得:BC⊥AE,BC⊥BE;
∴AE⊥平面BCE,则AE⊥BE…6分.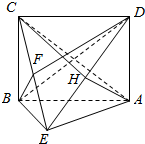
在Rt△BCE中,$CE=\sqrt{B{C^2}+B{E^2}}=\sqrt{{2^2}+{2^2}}=2\sqrt{2}$
同理可得:$DE=AB=CD=2\sqrt{2}$,$AC=2\sqrt{3}$;…8分.
∵AD=BC=AE=2.
∴取DE中点H,连结AH,CH,则AH⊥DE,CH⊥DE且$AH=\frac{1}{2}DE=\sqrt{2}$,$CH=\frac{{\sqrt{3}}}{2}DE=\sqrt{6}$…10分
∴∠CHA即为二面角C-DE-A的平面角;
在△CHA中,$cos∠CHA=\frac{{C{H^2}+A{H^2}-A{C^2}}}{2CH•AH}=\frac{{{{(\sqrt{6})}^2}+{{(\sqrt{2})}^2}-{{(2\sqrt{3})}^2}}}{{2\sqrt{6}•\sqrt{2}}}=-\frac{{\sqrt{3}}}{3}$;
∴二面角C-DE-A的余弦值为$-\frac{{\sqrt{3}}}{3}$.…12分.
点评 本题考查二面角的平面角的求法,直线与平面平行的判定定理的应用,考查空间想象能力、逻辑推理能力以及计算能力.

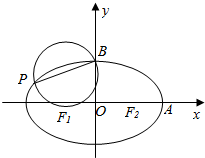 设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.
设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.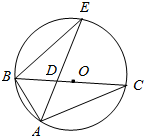 如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.
如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE. 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°. 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.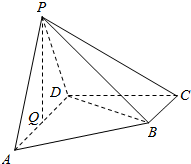 四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.
四棱锥P-ABCD中底面ABCD为直角梯形,AD∥BC,∠ADC=90°,面PAD⊥面ABCD,Q为AD的中点,PA=PD=2,AD=2BC=2,CD=$\sqrt{3}$.