题目内容
过抛物线y2=4x的焦点且与直线y=2x+1平行的直线方程是( )
A.y=-
| B.y=-
| C.y=2x-4 | D.y=2x-2 |
∵抛物线y2=4x中2p=4,得
=1,
∴抛物线的焦点为F(1,0),
又∵所求直线与直线y=2x+1平行,
∴直线的斜率k=2,得直线方程为y=2(x-1),
即y=2x-2.
故选D.
| p |
| 2 |
∴抛物线的焦点为F(1,0),
又∵所求直线与直线y=2x+1平行,
∴直线的斜率k=2,得直线方程为y=2(x-1),
即y=2x-2.
故选D.

练习册系列答案
相关题目
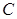 由上半椭圆
由上半椭圆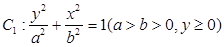 和部分抛物线
和部分抛物线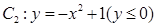 连接而成,
连接而成,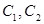 的公共点为
的公共点为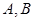 ,其中
,其中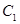 的离心率为
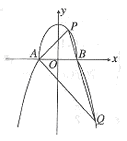
的离心率为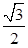 .
.
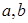 的值;
的值;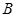 的直线
的直线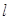 与
与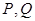 (均异于点
(均异于点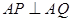 ,求直线
,求直线