题目内容
对于下列四个命题①若向量
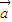 ,
,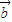 ,满足
,满足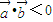 ,则
,则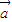 与
与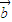 的夹角为钝角;
的夹角为钝角;②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下:
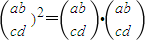 =
=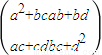 ,则
,则 =
=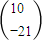
其中真命题是 (将你认为的正确命题的序号都填上).
【答案】分析:①根据向量夹角的范围和钝角的范围可以判断①的真假;
②利用长方体包含正四棱柱,进行判断;
③把点M(|a|,|a-3|)与N(cosα,sinα)分别代入x+y-2,判断x+y-2是否异号;
④利用已知定义进行代入计算验证.
解答:解:①当向量夹角为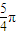 时,满足
时,满足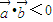 ,但不是钝角,故①错误;
,但不是钝角,故①错误;
②∵长方体底是长方形,正四棱柱底是正方形,∴A∩B=A,故②错误;
③∵|a|+|a-3|>2,cosα+sinα≤ <2,
<2,
∴a|+|a-3|-2>0,cosα+sinα-2<0,
∴点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧,故③正确;
④对2×2数表定义平方运算如下:
∴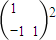 =
=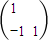
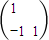 =
=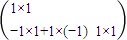 =
=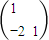
故答案为:③④.,
点评:此题考查的知识点比较多,有向量的计算,正四棱柱和长方体定义,集合之间的关系,以及矩阵的计算.
②利用长方体包含正四棱柱,进行判断;
③把点M(|a|,|a-3|)与N(cosα,sinα)分别代入x+y-2,判断x+y-2是否异号;
④利用已知定义进行代入计算验证.
解答:解:①当向量夹角为
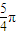 时,满足
时,满足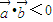 ,但不是钝角,故①错误;
,但不是钝角,故①错误;②∵长方体底是长方形,正四棱柱底是正方形,∴A∩B=A,故②错误;
③∵|a|+|a-3|>2,cosα+sinα≤
 <2,
<2,∴a|+|a-3|-2>0,cosα+sinα-2<0,
∴点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧,故③正确;
④对2×2数表定义平方运算如下:
∴
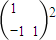 =
=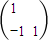
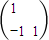 =
=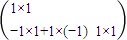 =
=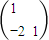
故答案为:③④.,
点评:此题考查的知识点比较多,有向量的计算,正四棱柱和长方体定义,集合之间的关系,以及矩阵的计算.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目