题目内容
对于四面体ABCD,给出下列四个命题:①若AB=AC,BD=CD,则BC⊥AD;②若AB=CD,AC=BD,则BC⊥AD;③若AB⊥AC,BD⊥CD,则BC⊥AD;④若AB⊥CD,BD⊥AC,则BC⊥AD.
其中真命题的序号是________.(写出所有真命题的序号)
答案:①④
解析:对于命题①,如图①,取BC的中点E,连结AE、DE,则BC⊥AE,BC⊥DE,
∴BC⊥AD.
对于命题④,如图②,过A向平面BCD作垂线AO,连结BO与CD交于点E,连结CO与BD交于点F,则CD⊥BE,同理,CF⊥BD.
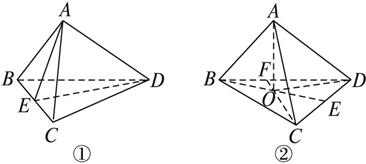
∴O为△BCD的垂心.连结DO,则BC⊥DO,BC⊥AO,
∴BC⊥AD.

练习册系列答案
相关题目