题目内容
过点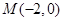 的直线
的直线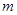 与椭圆
与椭圆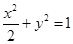 交于
交于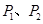 两点,线段
两点,线段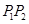 的中点为
的中点为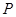 ,设直线
,设直线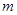 的斜率为
的斜率为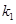 直线
直线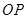 的斜率为
的斜率为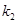 ,则
,则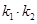 的值为
( )
的值为
( )
A . 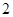 B.
B. 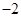 C.
C.  D .
D .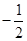
【答案】
D
【解析】

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
题目内容
过点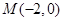 的直线
的直线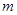 与椭圆
与椭圆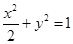 交于
交于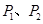 两点,线段
两点,线段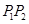 的中点为
的中点为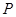 ,设直线
,设直线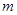 的斜率为
的斜率为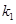 直线
直线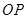 的斜率为
的斜率为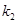 ,则
,则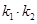 的值为
( )
的值为
( )
A . 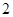 B.
B. 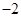 C.
C.  D .
D .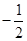
D
【解析】

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案