题目内容
设椭圆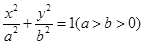 的左焦点为
的左焦点为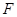 ,离心率为
,离心率为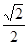 ,过点
,过点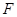 且与
且与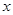 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为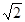 .
.
(1) 求椭圆方程.
(2) 过点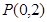 的直线
的直线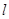 与椭圆交于不同的两点
与椭圆交于不同的两点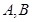 ,当
,当 面积最大时,求
面积最大时,求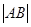 .
.
【答案】
(1) 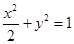 ;(2)
;(2) .
.
【解析】
试题分析:(1)由离心率得 ,由过点
,由过点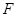 且与
且与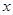 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为 得
得 ,再加椭圆中
,再加椭圆中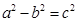 可解出
可解出 ,可得椭圆方程;(2)将直线方程设为
,可得椭圆方程;(2)将直线方程设为 ,交点设出,然后根据题意算出
,交点设出,然后根据题意算出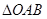 的面积
的面积 ,令
,令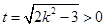 则
则 ,所以
,所以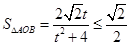 当且仅当
当且仅当 时等号成立,求出
时等号成立,求出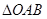 面积最大时的
面积最大时的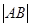 .
.
试题解析:(1)由题意可得 ,
, ,又
,又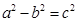 ,解得
,解得 ,所以椭圆方程为
,所以椭圆方程为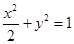 (4分)
(4分)
(2)根据题意可知,直线 的斜率存在,故设直线
的斜率存在,故设直线 的方程为
的方程为 ,设
,设 ,
, 由方程组
由方程组 消去
消去 得关于
得关于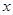 的方程
的方程 (6分)由直线
(6分)由直线 与椭圆相交于
与椭圆相交于 两点,则有
两点,则有 ,即
,即 得
得
由根与系数的关系得
故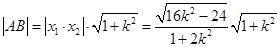 (9分)
(9分)
又因为原点 到直线
到直线 的距离
的距离 ,
,
故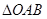 的面积
的面积
令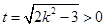 则
则 ,所以
,所以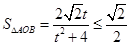 当且仅当
当且仅当 时等号成立,
时等号成立,
即 时,
时, (12分)
(12分)
考点:1.椭圆方程;2.椭圆与直线综合;3.基本不等式.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 的左焦点为
的左焦点为 ,离心率为
,离心率为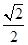 ,过点
,过点 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为
 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点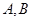 ,当
,当 面积最大时,求
面积最大时,求
 的左焦点为
的左焦点为 ,离心率为
,离心率为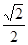 ,过点
,过点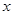 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为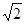 .
. 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点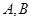 ,当
,当 面积最大时,求
面积最大时,求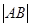 .
. 的左焦点为F, 离心率为
的左焦点为F, 离心率为 , 过点F且与x轴垂直的直线被椭圆截得的线段长为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为 .
. 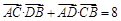 , 求k的值.
, 求k的值.