题目内容
20. 如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z•i(i是虚数单位)的共轭复数所对应的点为( )
如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z•i(i是虚数单位)的共轭复数所对应的点为( )| A. | Z1 | B. | Z2 | C. | Z3 | D. | Z4 |
分析 判断复数的几何意义,利用复数的乘法运算法则,推出结果即可.
解答 解:由题意可知复数z所对应的点为Z1,是虚部大于0的纯虚数,则复数z•i是负实数,
对应点在x负半轴,即Z2,共轭复数是Z2.
故选:B.
点评 本题考查复数的基本概念,复数的几何意义,考查计算能力.

练习册系列答案
相关题目
12.已知i是虚数单位.在复平面内,复数$\frac{1+i}{i}$的共轭复数对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.不等式x-x2>0的解集是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-1) | D. | (0,1) |
7. 如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB中点,则MN与平面PCD所成角的大小为( )
如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB中点,则MN与平面PCD所成角的大小为( )
 如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB中点,则MN与平面PCD所成角的大小为( )
如图所示,ABCD为矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB中点,则MN与平面PCD所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 某企业招聘大学生,经过综合测试,录用了14名女生和6名男生,这20名学生的测试成绩如茎叶图所示(单位:分),记成绩不小于80分者为A等,小于80分者为B等.
某企业招聘大学生,经过综合测试,录用了14名女生和6名男生,这20名学生的测试成绩如茎叶图所示(单位:分),记成绩不小于80分者为A等,小于80分者为B等.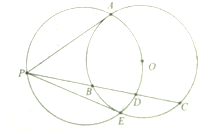 已知PA是圆O的切线,A为切点,割线PBC交圆O于B,C两点,D为BC中点.过点P,A,D的圆与圆O交于点E.
已知PA是圆O的切线,A为切点,割线PBC交圆O于B,C两点,D为BC中点.过点P,A,D的圆与圆O交于点E.