题目内容
8.在平面直角坐标系xOy中,点P(xP,yP)和点Q(xQ,yQ)满足$\left\{\begin{array}{l}{x_Q}={x_P}+{y_P}\;\\{y_Q}=-{x_P}+{y_P}\;\end{array}$按此规则由点P得到点Q,称为直角坐标平面的一个“点变换”.在此变换下,若$\frac{{|\overrightarrow{OP}|}}{{|\overrightarrow{OQ}|}}$=m,向量$\overrightarrow{OP}$与$\overrightarrow{OQ}$的夹角为θ,其中O为坐标原点,则msinθ的值为$\frac{1}{2}$.分析 先利用两点间的距离公式及已知的点变换公式,计算m的值,再利用向量夹角公式和点变换公式计算∠POQ=θ 的值,即可求出msinθ的值.
解答 解:依题意,($\frac{{|\overrightarrow{OP}|}}{{|\overrightarrow{OQ}|}}$)2=$\frac{{{x}_{Q}}^{2}+{{y}_{Q}}^{2}}{{{x}_{P}}^{2}+{{y}_{P}}^{2}}$=($\frac{1}{m}$)2
∵$\left\{\begin{array}{l}{x_Q}={x_P}+{y_P}\;\\{y_Q}=-{x_P}+{y_P}\;\end{array}$
∴$\frac{({x}_{P}+{y}_{P})^{2}+(-{x}_{P}+{y}_{P})^{2}}{{{x}_{P}}^{2}+{{y}_{P}}^{2}}$=($\frac{1}{m}$)2
∴m=$\frac{\sqrt{2}}{2}$
∵向量$\overrightarrow{OP}$与$\overrightarrow{OQ}$的夹角为θ,
∴cosθ=$\frac{\overrightarrow{OP}•\overrightarrow{OQ}}{|\overrightarrow{OP}||\overrightarrow{OQ}|}$=$\frac{1}{\sqrt{2}}$•$\frac{{{x}_{Q}}^{2}+{{y}_{Q}}^{2}}{{{x}_{P}}^{2}+{{y}_{P}}^{2}}$=$\frac{\sqrt{2}}{2}$
∴θ=$\frac{π}{4}$,
∴msinθ=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题综合考查了理解题意的能力,两点间的距离公式,向量夹角公式,具有较强的代数变换能力是解决本题的关键.

| A. | {-1,1}∪(-ln2,$-\frac{1}{3}$)∪($\frac{1}{3}$,ln2) | B. | [-1,$-\frac{1}{3}$)∪$({\frac{1}{3},1}]$ | ||
| C. | {-1,1}∪(-ln2,$-\frac{1}{2}$)∪($\frac{1}{2}$,ln2) | D. | ($-\frac{1}{2}$,$-\frac{1}{3}$)∪($\frac{1}{3}$,$\frac{1}{2}$) |
 如图,ABCDEF是变长为2的正六边形,以A为极点,射线AB为极轴建立极坐标系,若正六边形在极轴上方,在ρ≥0,θ∈[0,2π]的范围内,写出正六边形各个顶点的极坐标,并将它们化为直角坐标.
如图,ABCDEF是变长为2的正六边形,以A为极点,射线AB为极轴建立极坐标系,若正六边形在极轴上方,在ρ≥0,θ∈[0,2π]的范围内,写出正六边形各个顶点的极坐标,并将它们化为直角坐标. 如图,在三棱锥S-ABC中,BS=BA,SA⊥AC,D、E分别为SC、SA的中点.
如图,在三棱锥S-ABC中,BS=BA,SA⊥AC,D、E分别为SC、SA的中点.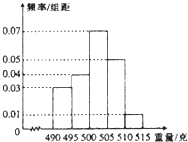 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40间产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40间产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示. 如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z•i(i是虚数单位)的共轭复数所对应的点为( )
如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z•i(i是虚数单位)的共轭复数所对应的点为( )