题目内容
12.已知函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$x2+ax+2,x∈[1,2]的图象上存在两点,在这两点处的切线互相垂直,则a的取值范围为(-6,-2).分析 求出函数的导数,求得两切点处的切线的斜率,运用两直线垂直的条件,结合二次函数的值域求法,对a讨论,考虑等式有解的条件,即可得到a的范围.
解答 解:函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$x2+ax+2的导数为f′(x)=x2+x+a,
设图象上两点(m,n),(s,t),且m,s∈[1,2],
即有两切线的斜率分别为k1=m2+m+a,k2=s2+s+a,
由在这两点处的切线互相垂直,可得k1k2=-1,
即有m2+m+a=$\frac{-1}{{s}^{2}+s+a}$,
由m∈[1,2],
则k1=m2+m+a=(m+$\frac{1}{2}$)2+a-$\frac{1}{4}$∈[a+2,a+6],
同样k2=s2+s+a∈[a+2,a+6],
当a≤-6时,k1≤0,k2≤0,不成立;
当a≥-2时,k1≥0,k2≥0,不成立;
当-6<a<-2时,k1,k2有正有负,等式成立,
即图象上存在两点,在这两点处的切线互相垂直.
故a的取值范围为(-6,-2).
故答案为:(-6,-2).
点评 本题考查导数的运用:求切线的斜率,同时考查两直线垂直的条件,二次函数在闭区间上的最值,运用分类讨论的思想方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
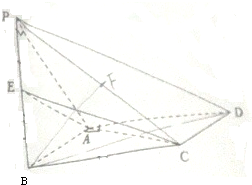 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PB的中点.