题目内容
6.已知四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?证明你的结论;
(Ⅲ)是否存在E点使得PA∥平面BDE?证明你的结论.
分析 (I)由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2.由锥体体积公式可求;
(II)不论点E在何位置,都有BD⊥AE;利用正方形和线面垂直的性质定理证明;
(Ⅲ)当E点为PC中点时,PA∥平面BDE;利用线面平行的判定定理证明.
解答 解:(I)由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2.
∴${V_{P-ABCD}}=\frac{1}{3}{S_{ABCD}}•PC=\frac{2}{3}$…(3分)
(II)不论点E在何位置,都有BD⊥AE.…(4分)
证明:连接AC,∵ABCD是正方形,∴BD⊥AC.∵PC⊥底面ABCD,且BD?平面ABCD,∴BD⊥PC.…(5分)
又AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE?平面PAC.
∴不论点E在何位置,都有BD⊥AE.…(8分)
(Ⅲ)当E点为PC中点时,PA∥平面BDE…(9分)
证明:连结AC交BD于O点,连结OE
∵四边形ABCD为正方形
∴O点为AC中点,又E点为PC中点
∴OE∥PA,又PA?平面BDE,OE?平面BDE
∴PA∥平面BDE…(12分)
点评 本题考查了锥体的三视图、体积公式以及线面垂直、线面平行的性质定理和判定定理的运用;属于中档题.

练习册系列答案
相关题目

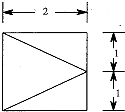 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.
已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$. 如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.
如图,已知PE切圆O于点E,割线PBA交圆O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.