Question

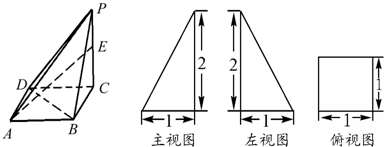
1．P是边长为2的正方形ABCD外一点，PD⊥面AC，O、E、F分别是AC、PA、PB中点．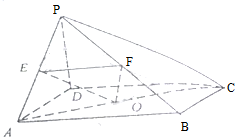
（1）求证：面EFO∥面PDC；
（2）求OE到面PDC的距离．

Answer 1

分析 （1）证明OE∥面PDC，EF∥面PDC，即可证明面EFO∥面PDC；
（2）OE到面PDC的距离为O到面PDC的距离，作OM⊥CD，垂足为D，则OM⊥面PDC，求出OM，即可得出结论．

解答 （1）证明：∵O、E是AC、PA的中点，
∴OE∥PC，
∵OE?面PDC，PC?面PDC，
∴OE∥面PDC，
同理EF∥面PDC，
∵OE∩EF=E，
∴面EFO∥面PDC；
（2）解：由（1）OE∥面PDC，
∴OE到面PDC的距离为O到面PDC的距离，
作OM⊥CD，垂足为D，则OM⊥面PDC，
∵O是AC的中点，ABCD是边长为2的正方形，
∴OM=1，
∴OE到面PDC的距离为1．

点评 本题考查线面平行、平面与平面平行的判定，考查点到平面距离的计算，正确运用线面平行、平面与平面平行的判定是关键．