题目内容
17.已知函数f(x)=$\frac{e^x}{{{x^2}-ax+1}}({a≥0})$.(e=2.71828…是自然对数的底数)(1)试讨论函数f(x)的单调区间;
(2)若不等式f(x)≥x对于任意的x∈[0,a+1]恒成立,求a的取值范围.
分析 (1)先求导$f'(x)=\frac{{{e^x}({x-1})[{x-({a+1})}]}}{{{{({{x^2}-ax+1})}^2}}}$,根据函数的定义域及导数的正负分a=0,a∈(0,2),a=2,a∈(2,+∞),讨论函数的定义域并求单调区间;
(2)结合(1)分a∈(2,+∞),a=2,a=0及a∈(0,2)讨论不等式f(x)≥x对于任意的x∈[0,a+1]恒成立是否成立,从而求a的取值范围.
解答 解:(1)$f'(x)=\frac{{{e^x}({x-1})[{x-({a+1})}]}}{{{{({{x^2}-ax+1})}^2}}}$,
①当a=0时,函数定义域为R,$f'(x)=\frac{{{e^x}{{({x-1})}^2}}}{{{{({{x^2}+1})}^2}}}≥0$,故f(x)在R上单调递增;
②当a∈(0,2)时,函数定义域为R,又a+1>1,
故f(x)在(-∞,1)单调递增,(1,1+a)单调递减,(1+a,+∞)单调递增;
③当a=2时,函数定义域为(-∞,1)∪(1,+∞),$f'(x)=\frac{{{e^x}({x-3})}}{x-1}$,
故f(x)在(-∞,1)单调递增,(1,3)单调递减,(3,+∞)单调递增;
④当a∈(2,+∞)时,方程x2-ax+1=0的两个根为${x_1}=\frac{{a-\sqrt{{a^2}-4}}}{2},{x_2}=\frac{{a+\sqrt{{a^2}-4}}}{2}$,
所以函数的定义域为(-∞,x1)∪(x1,x2)∪(x2,+∞),
由韦达定理知0<x1<1<x2,
对称轴$x=\frac{a}{2}<a+1$,(a+1)2-a(a+1)+1=a+2>0,故x2<a+1,
f(x)在(-∞,x1),(x1,1),(1+a,+∞)单调递增,(1,x2),(x2,a+1)单调递减;
(2)①当a∈(2,+∞)时,x∈[x1,x2]⊆[0,a+1]时,有f(x)<0即f(x)≥x不成立;
②当a=2时,由(1)可知不符合题意;
③当a=0时,f(x)单调递增,fmin(x)=f(0)=1,故不等式恒成立;
④当a∈(0,2)时,$f(0)=1,f(1)=\frac{e}{2-a}>1,f({1+a})=\frac{{{e^{a+1}}}}{a+2}$,
下面证明$f({1+a})=\frac{{{e^{a+1}}}}{a+2}≥a+1$,
即证ex-x(x+1)≥0(x=a+1∈(1,3)),
令g(x)=ex-x(x+1),g′(x)=ex-2x-1,g″(x)=ex-2,
∵x∈(1,3),∴g″(x)>0,g′(x)单调递增,g′(1)<0,g′(3)>0,
∴?x0使得$g'({x_0})={e^{x_0}}-2{x_0}-1=0$,
g(x)在(1,x0)上单调递减,在(x0,3)上单调递增,
此时$g(x)≥g({x_0})={e^{x_0}}-x_0^2-{x_0}=-x_0^2+{x_0}+1$,
$g'({\frac{{1+\sqrt{5}}}{2}})={e^{\frac{{1+\sqrt{5}}}{2}}}-({2+\sqrt{5}})>0$,
∴${x_0}<\frac{{1+\sqrt{5}}}{2}$,
∴g(x0)>0;
所以不等式ex-x(x+1)≥0(x=a+1∈(1,3))成立.
即$f({1+a})=\frac{{{e^{a+1}}}}{a+2}≥a+1$;
由(1)知f(x)在(0,1)单调递增,(1,1+a)单调递减,
所以不等式f(x)≥x对于任意的x∈[0,a+1]恒成立
综上所述,
当a∈[0,2)时,不等式f(x)≥x对于任意的x∈[0,a+1]恒成立.
点评 本题考查了导数的综合应用及恒成立问题的处理方法,同时考查了分类讨论的思想及单调性的判断与应用,化简及分类讨论比较困难,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
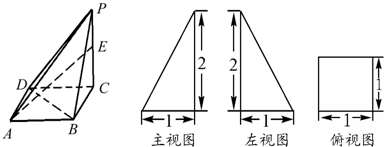
小学生10分钟应用题系列答案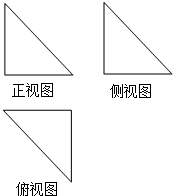 已知某几何体的三视图都是全等的等腰直角三角形,直角边长为1,如图所示,则该几何体的表面积是( )
已知某几何体的三视图都是全等的等腰直角三角形,直角边长为1,如图所示,则该几何体的表面积是( )| A. | $1+\sqrt{2}$ | B. | 2 | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}+\sqrt{2}$ |
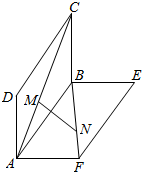 如图所示,四边形ABCD、ABEF都是矩形,它们所在的平面互相垂直,AD=AF=1,AB=2,点M、N分别在它们的对角线AC、BF上,且CM=BN=a(0<a<$\sqrt{5}$),当MN的长最小时,a的值为( )
如图所示,四边形ABCD、ABEF都是矩形,它们所在的平面互相垂直,AD=AF=1,AB=2,点M、N分别在它们的对角线AC、BF上,且CM=BN=a(0<a<$\sqrt{5}$),当MN的长最小时,a的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{10}}{3}$ |
| A. | (-$\frac{1}{3}$,$\frac{1}{3}$) | B. | (-$\frac{1}{3}$,$\frac{1}{5}$) | C. | ($\frac{1}{5}$,$\frac{1}{3}$) | D. | (-$\frac{1}{3}$.$\frac{1}{5}$)∪($\frac{1}{5}$,$\frac{1}{3}$) |
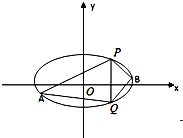 已知椭圆C的中心在原点,焦点在X轴上,离心率等于$\frac{1}{2}$,它的两个顶点恰好是双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点.
已知椭圆C的中心在原点,焦点在X轴上,离心率等于$\frac{1}{2}$,它的两个顶点恰好是双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点.