题目内容
求通过两条直线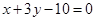 和
和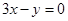 的交点,且距原点距离为1的直线方程。
的交点,且距原点距离为1的直线方程。
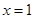 或
或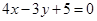
解析试题分析:由方程组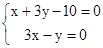
解得两条直线的交点为A(1,3)
当直线的斜率存在时,设所求直线的方程为:y-3=k(x-1),即kx-y+3-k=0
由点到直线的距离公式可得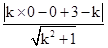 =1,解得k=
=1,解得k=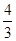 ,
,
即直线方程为:4x-3y+5=0,
当直线的斜率不存在时,直线的方程为x=1也符合题意,
故所求直线的方程为:4x-3y+5=0或x=1.
考点:两直线的位置关系,点到直线的距离公式。
点评:中档题,本题解答思路明确,通过建立方程组,确定交点坐标,进一步利用点到直线的距离公式,建立直线斜率k的方程组。本题易错---漏解,注意结合图形,分析直线的条数。

练习册系列答案
相关题目
 并且和
并且和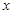 轴的正半轴、
轴的正半轴、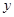 轴的正半轴所围成的三角形的面积是
轴的正半轴所围成的三角形的面积是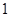 的直线方程.
的直线方程.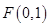 直线
直线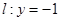 ,
,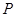 为平面上的动点,过点
为平面上的动点,过点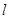 的垂线,垂足为
的垂线,垂足为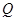 ,且
,且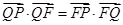 .
. 、
、 是轨迹
是轨迹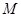 上异于坐标原点
上异于坐标原点 的不同两点,轨迹
的不同两点,轨迹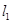 、
、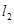 ,且
,且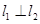 ,
,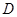 ,求点
,求点 的直线方程.
的直线方程. :
: ,
, :
: .
. ,求实数
,求实数 的值;(2)当
的值;(2)当 时,求直线
时,求直线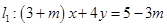 ,
,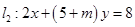 ;
; 为何值时,
为何值时,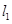 与
与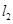 (1)相交;(2)平行;(3)垂直.
(1)相交;(2)平行;(3)垂直. 作直线
作直线 ,使它被两相交直线
,使它被两相交直线 和
和 所截得的线段
所截得的线段 恰好被
恰好被 点平分,求直线
点平分,求直线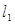 :
: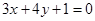 和点
和点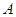 (1,2).设过
(1,2).设过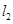 .
. 被两平行直线
被两平行直线 和
和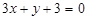 所截得的线段长为9,且直线过点
所截得的线段长为9,且直线过点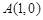 ,求直线
,求直线