Question

（本题满分16分）已知,

且.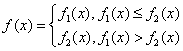

(Ⅰ)当时,求在处的切线方程；

(Ⅱ)当时,设所对应的自变量取值区间的长度为(闭区间的长度定义为),试求的最大值；

(Ⅲ)是否存在这样的，使得当时,?若存在,求出的取值范围；若不存在，请说明理由.

 

 

Answer 1

解: (Ⅰ)当时,.

因为当时,,,

且,

所以当时,,且………………………………(3分)

由于,所以,又,

故所求切线方程为,

即………………………………………………………………(5分)

   (Ⅱ) 因为,所以,则

当时,因为,,

所以由,解得,

从而当时, …………………………………………(6分)

当时,因为,,

所以由,解得,

从而当时, ………………………………………(7分)

③当时,因为,

从而 一定不成立……………………………………………………………(8分)

综上得,当且仅当时,,

故 ………………………………………(9分)

从而当时,取得最大值为………………………………………………(10分)

(Ⅲ)“当时,”等价于“对恒成立”,

即“(*)对恒成立” ……………………………(11分)

当时,,则当时,,则(*)可化为

,即,而当时,,

所以,从而适合题意……………………………………………………………(12分)

当时,.

当时,(*)可化为,即,而,

所以,此时要求………………………………………………………(13分)

当时,(*)可化为,

所以,此时只要求……………………………………………………(14分)

(3)当时,(*)可化为,即,而,

所以,此时要求………………………………………………………(15分)

由⑴⑵⑶,得符合题意要求.

 综合①②知,满足题意的存在,且的取值范围是……………………………(16分)