题目内容
 如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.(1)当
 |
| CN |
| 1 |
| 4 |
 |
| MN |
(2)求矩形ABCD的面积的最大值.
考点:扇形面积公式
专题:计算题,三角函数的图像与性质
分析:(1)由题意可得,∠NOC=30°,由对称性,可知,∠COE=30°,则△DOC为等腰三角形,且CD=OD,通过解直角三角形,即可得到;
(2)设∠COE=α,设OE交AD于E,交BC于F,显然矩形ABCD关于OE对称,而E,F均为AD,BC的中点,先把矩形的各个边长用角α表示出来,进而表示出矩形的面积,再利用角α的范围来求出矩形面积的最大值即可.
(2)设∠COE=α,设OE交AD于E,交BC于F,显然矩形ABCD关于OE对称,而E,F均为AD,BC的中点,先把矩形的各个边长用角α表示出来,进而表示出矩形的面积,再利用角α的范围来求出矩形面积的最大值即可.
解答:
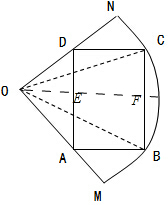 解:(1)当
解:(1)当
=
时,即有∠NOC=30°,
由对称性,可知,∠COE=30°,
则△DOC为等腰三角形,且CD=OD,
由等腰三角形的三线合一,则CDcos30°=1,
解得,CD=
;
(2)设∠COE=α,
设OE交AD于E,交BC于F,显然矩形ABCD关于OE对称,
而E,F均为AD,BC的中点,在Rt△OFC中,CF=2sinα,OF=2cosα.
则BC=AD=4sinα,OE=OF-EF=2cosα-CD,DE=OEtan60°=
OE=2sinα,
即有CD=2cosα-
sinα,
则矩形ABCD的面积S=CD•BC=(2cosα-
sinα)•4sinα
=8sinαcosα-
sin2α=4sin2α-
(1-cos2α)
=
(
sin2α+
cos2α)-
=
sin(2α+
)-
,
当sin(2α+
)=1即α=
时,面积取得最大值,且为
.
 解:(1)当
解:(1)当 |
| CN |
| 1 |
| 4 |
 |
| MN |
由对称性,可知,∠COE=30°,
则△DOC为等腰三角形,且CD=OD,
由等腰三角形的三线合一,则CDcos30°=1,
解得,CD=
2
| ||
| 3 |
(2)设∠COE=α,
设OE交AD于E,交BC于F,显然矩形ABCD关于OE对称,
而E,F均为AD,BC的中点,在Rt△OFC中,CF=2sinα,OF=2cosα.
则BC=AD=4sinα,OE=OF-EF=2cosα-CD,DE=OEtan60°=
| 3 |
即有CD=2cosα-
2
| ||
| 3 |
则矩形ABCD的面积S=CD•BC=(2cosα-
2
| ||
| 3 |
=8sinαcosα-
8
| ||
| 3 |
4
| ||
| 3 |
=
8
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
8
| ||
| 3 |
| π |
| 6 |
4
| ||
| 3 |
当sin(2α+
| π |
| 6 |
| π |
| 6 |
4
| ||
| 3 |
点评:本题主要考查解三角形的有关知识在实际生活中的应用问题;解决这一类型题目的关键在与把文字语言转化为数学表达式,最终利用数学知识解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某地区300家商店中,有大型商店30家,中型商店75家,其余的为小型商店,为了掌握各商店的营业情况,要从中抽取一个容量为40的样本.若采用分层抽样的方法,则抽取的中型商店数是( )
| A、4 | B、5 | C、10 | D、26 |
如图框图属于( )
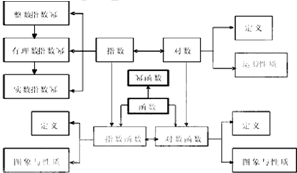

| A、程序框图 | B、工序流程图 |
| C、知识结构图 | D、组织结构图 |
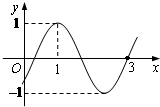 已知函数f(x)=sin(ωx+φ)(ω>0)的图象如右图所示,则f(2)=
已知函数f(x)=sin(ωx+φ)(ω>0)的图象如右图所示,则f(2)=