题目内容
为加强中学生实践、创新能力和团队精神的培养，促进教育教学改革，教育部门主办了全国中学生航模竞赛．该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序．通过预赛，选拔出甲、乙、丙和丁四支队伍参加决赛．
（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；
（ II）求决赛中甲、乙两支队伍出场顺序相邻的概率．
解：利用树状图列举如右图，这是以甲开头的，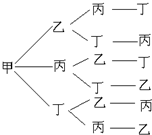
还有分别以乙、丙、丁开头的也都有6种情况．
故总共有24个基本事件，
符合（Ⅰ）要求的有4个基本事件，符合（ II）要求的有12个基本事件，
所以所求的概率分别为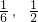
．
另解：（Ⅰ）由排列组合的公式可得“甲、乙两支队伍恰好排在前两位”的概率P=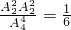
（ II）同理可得，“甲、乙两支队伍出场顺序相邻”的概率为
分析：列举总的基本事件数，设“甲、乙两支队伍恰好排在前两位”为事件A，“甲、乙两支队伍出场顺序相邻”为事件B，分析可得A、B包含的基本事件数目，由等可能事件的概率公式，计算可得答案．
点评：本题考查等可能事件概率的计算，关键是根据题意，正确列举基本事件空间，得到其包含基本事件的数目．
还有分别以乙、丙、丁开头的也都有6种情况．
故总共有24个基本事件，
符合（Ⅰ）要求的有4个基本事件，符合（ II）要求的有12个基本事件，
所以所求的概率分别为
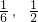．另解：（Ⅰ）由排列组合的公式可得“甲、乙两支队伍恰好排在前两位”的概率P=
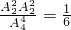
（ II）同理可得，“甲、乙两支队伍出场顺序相邻”的概率为
分析：列举总的基本事件数，设“甲、乙两支队伍恰好排在前两位”为事件A，“甲、乙两支队伍出场顺序相邻”为事件B，分析可得A、B包含的基本事件数目，由等可能事件的概率公式，计算可得答案．
点评：本题考查等可能事件概率的计算，关键是根据题意，正确列举基本事件空间，得到其包含基本事件的数目．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，正弦函数图象的相应的解析式为________．
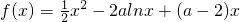，a∈R．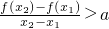
恒成立，若存在求出a的取值范围，若不存在，说明理由．
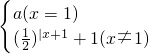，若关于x的方程2f2（x）-（2a+3）f（x）+3a=0有五个不同的实数解，则们组题意的a的取值范围是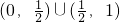
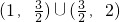
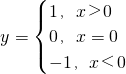，试编写算法，画出流程图，写出程序输入x的值，输出y的值．
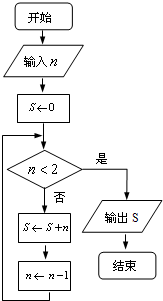阅读如图所示的程序框，若输入的n是100，则输出的变量S的值是
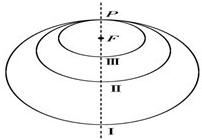如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行，若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：
．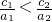