题目内容

定义在(0，＋∞)的三个函数f(x)、g(x)、h(x)，已知f(x)＝lnx，g(x)＝x2－af(x)，h(x)＝x－a，且g(x)在x＝1处取极值．

(Ⅰ)求a值及h(x)的单调区间；

(Ⅱ)求证：当1＜x＜e2时，恒有

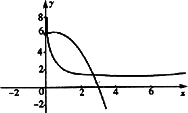
(Ⅲ)把h(x)对应的曲线C1向上平移6个单位后得曲线C2，求C2与g(x)对应曲线C3的交点个数，并说明道理．

答案：
解析：

　　解(Ⅰ)由题意：

　　∴a＝2　　2分

　　而所以h(x)在上为增函数，h(x)在上为增函数．　　4分

　　(Ⅱ)

　　欲证：只需证：，即证：

　　记

　　∴

　　∴当x＞1时，为增函数　　9分

　　

　　即

　　∴结论成立　　10分

　　(Ⅲ)由(1)知：

　　∴对应表达式为

　　∴问题转化成求函数

　　即求方程：

　　即：

　　设

　　∴当时，为减函数．

　　当时，为增函数．

　　而的图象开口向下的抛物线

　　∴与的大致图象如图：

　　∴与的交点个数为2个．即与的交点个数为2个　　16分


练习册系列答案
相关题目
已知定义在[0，+∞）上的函数f（x）满足f（x）=3f（x+2），当x∈[0，2）时，f（x）=-x2+2x，设f（x）在[2n-2，2n）上的最大值为an（n∈N+）且{an}的前n项和为Sn，则
lim
n→∞
Sn=（　　）
A、3
B、
5
2
C、2
D、
3
2
函数f（x）是定义在[0，1]上的增函数，满足f(x)=2f(
x
2
)且f（1）=1，在每个区间(
1
2i
，
1
2i-1
]（i=1，2…）上，y=f（x）的图象都是斜率为同一常数k的直线的一部分．
（1）求f（0）及f(
1
2
)，f(
1
4
)的值，并归纳出f(
1
2i
)(i=1，2，…)的表达式
（2）设直线x=
1
2i
，x=
1
2i-1
，x轴及y=f（x）的图象围成的矩形的面积为ai（i=1，2…），记S(k)=
lim
n→∞
(a1+a2+…+an)，求S（k）的表达式，并写出其定义域和最小值．
若函数f（x）为定义在[0，+∞）上的增函数，定义在R上的函数g（x）满足g（x）=f（|x|），则不等式g(
2x
)＞g(1)的解集为
（-2，0）∪（0，2）
（-2，0）∪（0，2）
．
（2013•闵行区一模）已知定义在(0，
π
2
)上的函数y=2（sinx+1）与y=
8
3
的图象的交点为P，过P作PP1⊥x轴于P1，直线PP1与y=tanx的图象交于点P2，则线段P1P2的长为
2
4
2
4
．
若f（x）是定义在[0，+∞）上的增函数，则不等式f(2x-1)＜f(
13
)的解集为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网