题目内容
已知函数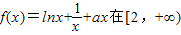 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 .
【答案】分析:根据题意,已知f(x)在区间[2,+∞)上是减函数,即f′(x)≤0在区间[2,+∞)上恒成立,对于恒成立往往是把字母变量放在一边即参变量分离,另一边转化为求函数在定义域下的最值,即可求解.
解答:解:f′(x)=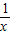 -
-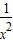 +a,,∵f(x)在[2,+∞)上为减函数,
+a,,∵f(x)在[2,+∞)上为减函数,
∴x∈[2,+∞)时,f′(x)=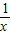 -
-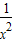 +a≤0恒成立.
+a≤0恒成立.
即a≤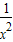 -
-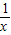 恒成立.
恒成立.
设y=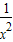 -
-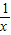 ,
,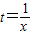 ∈(0,
∈(0, ]
]
y=t2-t=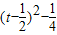 ≥
≥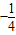
∴ymin=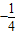
则a≤ymin=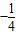
故答案为: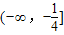
点评:本题主要考查了根据函数单调性求参数范围的问题,解题的关键将题目转化成f′(x)≤0在区间[2,+∞)上恒成立进行求解,同时考查了参数分离法,属于中档题.
解答:解:f′(x)=
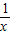 -
-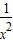 +a,,∵f(x)在[2,+∞)上为减函数,
+a,,∵f(x)在[2,+∞)上为减函数,∴x∈[2,+∞)时,f′(x)=
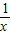 -
-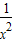 +a≤0恒成立.
+a≤0恒成立.即a≤
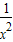 -
-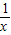 恒成立.
恒成立.设y=
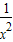 -
-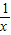 ,
,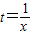 ∈(0,
∈(0, ]
]y=t2-t=
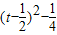 ≥
≥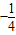
∴ymin=
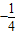
则a≤ymin=
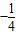
故答案为:
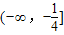
点评:本题主要考查了根据函数单调性求参数范围的问题,解题的关键将题目转化成f′(x)≤0在区间[2,+∞)上恒成立进行求解,同时考查了参数分离法,属于中档题.

练习册系列答案
相关题目
 )上是减函数,求实数m的取值范围.
)上是减函数,求实数m的取值范围.