题目内容
已知函数f(x)=lg(x2-mx-m).(1)若m=1,求函数f(x)的定义域;
(2)若函数f(x)的值域为R,求实数m的取值范围;
(3)若函数f(x)在区间(-∞,1-
 )上是减函数,求实数m的取值范围.
)上是减函数,求实数m的取值范围.
【答案】分析:(1) ,由此能求出其定义域.
,由此能求出其定义域.
(2)由于f(x)值城为R,因此其真数N(x)=x2-mx-m应能取遍所有的正数,结合二次函数N(x)图象能求出m的范围.
(3)因y=lgx在其定义城上为增,则N(x)=x2-mx-m应在相应定义区间上为单调函数,结合二次函数图象的对称轴与区间位置分析,能够推导出实数m的取值范围.
解答:解:(1)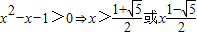 ,因此其定义域为
,因此其定义域为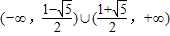
(2)由于f(x)值城为R,因此其真数N(x)=x2-mx-m应能取遍所有的正数,结合二次函数N(x)图象易知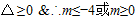 ,即m∈(-∞,-4]∪[0,+∞).
,即m∈(-∞,-4]∪[0,+∞).
(3)因y=lgx在其定义城上为增,则N(x)=x2-mx-m应在相应定义区间上为单调函数,结合二次函数图象的对称轴与区间位置分析,其对称轴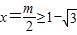 ①同时必须考虑N(x)=x2-mx-m在
①同时必须考虑N(x)=x2-mx-m在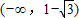 上为正,故
上为正,故 ②综合①、②式可得
②综合①、②式可得 ∴
∴
点评:本题考查对数函数的定义域、值域、最值和单调性的应用,解题时要充分运用对数函数的性质求解.
 ,由此能求出其定义域.
,由此能求出其定义域.(2)由于f(x)值城为R,因此其真数N(x)=x2-mx-m应能取遍所有的正数,结合二次函数N(x)图象能求出m的范围.
(3)因y=lgx在其定义城上为增,则N(x)=x2-mx-m应在相应定义区间上为单调函数,结合二次函数图象的对称轴与区间位置分析,能够推导出实数m的取值范围.
解答:解:(1)
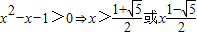 ,因此其定义域为
,因此其定义域为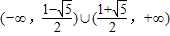
(2)由于f(x)值城为R,因此其真数N(x)=x2-mx-m应能取遍所有的正数,结合二次函数N(x)图象易知
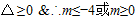 ,即m∈(-∞,-4]∪[0,+∞).
,即m∈(-∞,-4]∪[0,+∞).(3)因y=lgx在其定义城上为增,则N(x)=x2-mx-m应在相应定义区间上为单调函数,结合二次函数图象的对称轴与区间位置分析,其对称轴
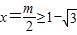 ①同时必须考虑N(x)=x2-mx-m在
①同时必须考虑N(x)=x2-mx-m在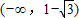 上为正,故
上为正,故 ②综合①、②式可得
②综合①、②式可得 ∴
∴
点评:本题考查对数函数的定义域、值域、最值和单调性的应用,解题时要充分运用对数函数的性质求解.

练习册系列答案
相关题目