题目内容
已知函数f(x)=
x3-
nx2+mx,x∈R,
(1)若f(x)的单调减区间是(1,2),求f(x)的零点;
(2)若0<m<3,0<n<3,求f(x)在区间(1,2)上是减函数的概率.
| 1 |
| 3 |
| 1 |
| 2 |
(1)若f(x)的单调减区间是(1,2),求f(x)的零点;
(2)若0<m<3,0<n<3,求f(x)在区间(1,2)上是减函数的概率.
分析:(1)求出函数的导函数,由函数的减区间为(1,2),可知导函数对应方程的两根为1,2,利用跟与系数的关系列式可求n和m的值,代入原函数后求解对应的3次方程可得函数f(x)的零点;
(2)函数f(x)在区间(1,2)上是减函数,说明其导函数在x∈(1,2)时小于0恒成立,结合二次函数的图象列出关于m,n的不等式组,即得到关于m,n的约束条件,建系后找出可行域,利用几何概型可求f(x)在区间(1,2)上是减函数的概率.
(2)函数f(x)在区间(1,2)上是减函数,说明其导函数在x∈(1,2)时小于0恒成立,结合二次函数的图象列出关于m,n的不等式组,即得到关于m,n的约束条件,建系后找出可行域,利用几何概型可求f(x)在区间(1,2)上是减函数的概率.
解答:解:(1)由f′(x)=
x3-
nx2+mx,得:f′(x)=x2-nx+m,
∵f(x)的单调减区间是(1,2)∴方程x2-nx+m=0的两根为1和2,
∴
∴
,∴f(x)=
x3-
x2+2x.
令f(x)=0,即
x3-
x2+2x=0,得x=0或
x2-
x+2=0(*)
对于方程(*),其判别式△=(-
)2-4×
×2=-
<0,∴该方程无解.
∴函数f(x)的零点为0.
(2)f′(x)=x2-nx+m,若f(x)在区间(1,2)上为减函数,则f′(x)<0对x∈(1,2)恒成立,
由f′(x)是开口向上抛物线,所以
,即
,
建立直角坐标系,横轴为n轴,纵轴为m轴.
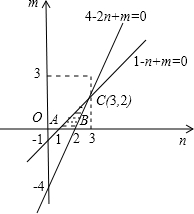
直线1-n+m=0与n轴交点为A(1,0),
直线4-2n+m=0与n轴交点为B(2,0),
求解方程组
⇒
,即交点C(3,2).
所以,满足条件的可行域为图中阴影部分,
可行区域面积为
×1×2=1,
故f(x)在区间(1,2)上是减函数的概率P=
=
.
| 1 |
| 3 |
| 1 |
| 2 |
∵f(x)的单调减区间是(1,2)∴方程x2-nx+m=0的两根为1和2,
∴
|
|
| 1 |
| 3 |
| 3 |
| 2 |
令f(x)=0,即
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
对于方程(*),其判别式△=(-
| 3 |
| 2 |
| 1 |
| 3 |
| 5 |
| 12 |
∴函数f(x)的零点为0.
(2)f′(x)=x2-nx+m,若f(x)在区间(1,2)上为减函数,则f′(x)<0对x∈(1,2)恒成立,
由f′(x)是开口向上抛物线,所以
|
|
建立直角坐标系,横轴为n轴,纵轴为m轴.

直线1-n+m=0与n轴交点为A(1,0),
直线4-2n+m=0与n轴交点为B(2,0),
求解方程组
|
|
所以,满足条件的可行域为图中阴影部分,
可行区域面积为
| 1 |
| 2 |
故f(x)在区间(1,2)上是减函数的概率P=
| 1 |
| 3×3 |
| 1 |
| 9 |
点评:本题考查了利用导函数研究函数的单调性,考查了导函数的零点与原函数单调区间之间的关系,考查了函数零点的求法,训练了数形结合求解几何概型题,解答此题的关键是找准测度比,此题是中高档题.

练习册系列答案
相关题目