题目内容
已知椭圆C: +
+ =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P( ,
, ).
).
(1)求椭圆C的方程;
(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,2 ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
(1) 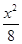 +
+ =1 (2) 直线QG与椭圆C一定有唯一的公共点,理由见解析
=1 (2) 直线QG与椭圆C一定有唯一的公共点,理由见解析
解析解:(1)因为焦距为4,
所以a2-b2=4.
又因为椭圆C过点P( ,
, ),
),
所以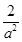 +
+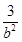 =1,
=1,
故a2=8,b2=4,
从而椭圆C的方程为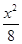 +
+ =1.
=1.
(2)一定有唯一的公共点.
由题意,E点坐标为(x0,0).
设D(xD,0),则 =(x0,-2
=(x0,-2 ),
),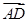 =(xD,-2
=(xD,-2 ).
).
再由AD⊥AE知, 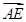 ·
·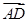 =0,
=0,
即xDx0+8=0.
由于x0y0≠0,故xD=-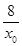 .
.
因为点G是点D关于y轴的对称点,所以点G(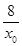 ,0).
,0).
故直线QG的斜率kQG=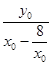 =
= .
.
又因Q(x0,y0)在椭圆C上,
所以 +2
+2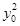 =8.①
=8.①
从而kQG=-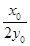 .
.
故直线QG的方程为
y=-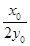 (x-
(x-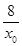 ).②
).②
将②代入椭圆C方程,得
( +2
+2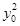 )x2-16x0x+64-16
)x2-16x0x+64-16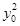 =0.③
=0.③
再将①代入③,化简得
x2-2x0x+ =0.
=0.
解得x=x0,y=y0,
即直线QG与椭圆C一定有唯一的公共点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
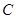 的中心在原点,焦点在
的中心在原点,焦点在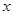 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的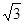 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为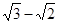
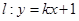 交椭圆
交椭圆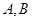 两点,当
两点,当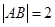 时求直线
时求直线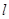 的方程
的方程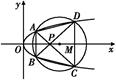
 .
. 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标. 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点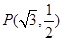 ,离心率是
,离心率是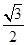 .
.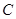 的标准方程;
的标准方程;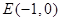 且与椭圆
且与椭圆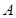 ,
,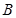 两点,若
两点,若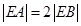 ,求直线的方程.
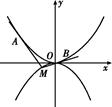
,求直线的方程. 时,切线MA的斜率为-
时,切线MA的斜率为- .
.
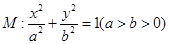 的离心率为
的离心率为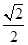 ,且经过点
,且经过点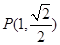 过坐标原点的直线
过坐标原点的直线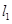 与
与 均不在坐标轴上,
均不在坐标轴上, =1(m>1)的左焦点为F1.若直线l与椭圆C交于A,B两点,满足
=1(m>1)的左焦点为F1.若直线l与椭圆C交于A,B两点,满足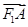 ·
·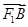 =0,求实数m的值.
=0,求实数m的值.