题目内容
已知椭圆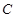 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点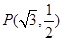 ,离心率是
,离心率是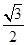 .
.
(1)求椭圆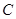 的标准方程;
的标准方程;
(2)直线过点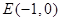 且与椭圆
且与椭圆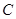 交于
交于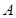 ,
,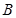 两点,若
两点,若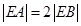 ,求直线的方程.
,求直线的方程.
(1)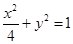 ;(2)
;(2)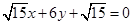 和
和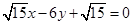 .
.
解析试题分析:(1)由题设条件知关于a,b,c的方程组,由此能求出椭圆方程.
(2)可以设直线方程(斜率不存在单独考虑),然后与椭圆方程联立,消去y得到关于x的一元二次方程,利用韦达定理结合题目条件建立方程即可求出直线方程.
试题解析:(1)设椭圆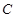 的方程为
的方程为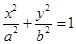
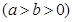 .
.
由已知可得 3分
3分
解得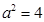 ,
,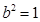 .
.
故椭圆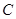 的方程为
的方程为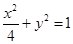 . 6分
. 6分
(2)由已知,若直线的斜率不存在,则过点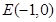 的直线的方程为
的直线的方程为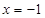 ,
,
此时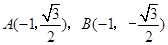 ,显然
,显然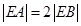 不成立. 7分
不成立. 7分
若直线的斜率存在,则设直线的方程为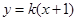 .
.
则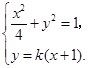
整理得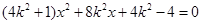 . 9分
. 9分
由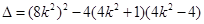
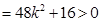 .
.
设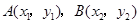 .
.
故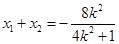 ,①
,① 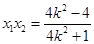 . ② 10分
. ② 10分
因为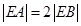 ,即
,即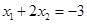 .③
.③
①②③联立解得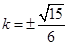 . 13分
. 13分
所以直线的方程为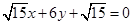 和
和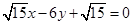 . 14分
. 14分
考点:(1)椭圆标准方程;(2)直线与圆锥曲线的位置关系.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.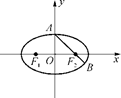
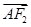 =2
=2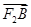 ,
,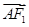 ·
· =
=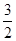 ,求椭圆的方程.
,求椭圆的方程. +
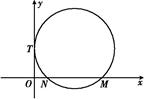
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点( ,
, ).
).
 +
+ =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P( ,
, ).
).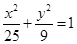 ,直线
,直线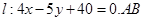 是直线上的线段,且
是直线上的线段,且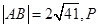 是椭圆上一点,求
是椭圆上一点,求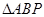 面积的最小值。
面积的最小值。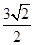 ,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.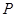 在椭圆
在椭圆 :
: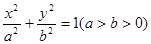 上,以
上,以 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点 ,且
,且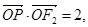
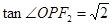 ,其中
,其中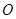 为坐标原点.
为坐标原点. ,设
,设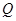 是椭圆
是椭圆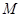 两点的直线
两点的直线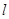 交
交 轴于点
轴于点 ,若
,若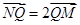 , 求直线
, 求直线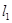 与椭圆
与椭圆 :
: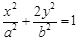 交于不同的两点
交于不同的两点 ,
, ,其中
,其中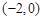 ,若点
,若点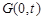 是线段
是线段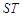 垂直平分线上一点,且满足
垂直平分线上一点,且满足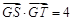 ,求实数
,求实数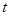 的值.
的值.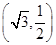 ,离心率是
,离心率是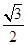 .
.