题目内容
如图,在四棱锥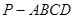 中,
中,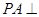 平面
平面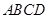 ,底面
,底面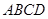 是菱形,
是菱形,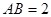 ,
,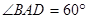 .
.

(Ⅰ)求证: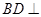
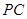 ;
;
(Ⅱ)若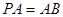 ,求二面角
,求二面角 的余弦值.
的余弦值.
【答案】
(Ⅰ)先证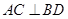 ,
,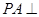
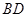 ,进而证明
,进而证明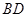 ⊥平面
⊥平面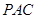 ,从而得证;
,从而得证;
(Ⅱ)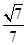
【解析】
试题分析:(Ⅰ)证明:因为四边形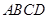 是菱形,所以
是菱形,所以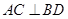 .
.
又因为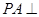 平面
平面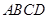 ,所以
,所以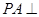
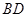 .
.
又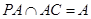 ,所以
,所以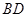 ⊥平面
⊥平面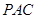 .
.
又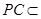 平面
平面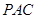 ,所以
,所以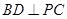 ……6分
……6分
(Ⅱ)依题意,知

平面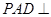 平面
平面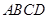 ,交线为
,交线为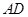 ,
,
过点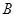 作
作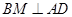 ,垂足为
,垂足为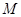 ,则
,则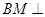 平面
平面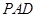 .
.
在平面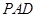 内过
内过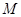 作
作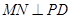 ,垂足为
,垂足为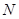 ,连
,连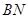 ,
,
则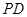 ⊥平面
⊥平面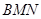 ,所以
,所以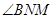 为二面角
为二面角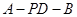 的一个平面角
. ……9分
的一个平面角
. ……9分
∵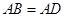 ,
,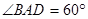 ,
,
∴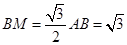 ,
, 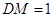 . ……10分
. ……10分
又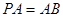 ,故
,故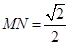 . 所以
. 所以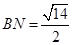 . ……11分
. ……11分
∴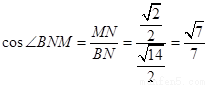 .
.
即二面角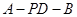 的余弦值为
的余弦值为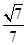 . ……12分
. ……12分
考点:本小题主要考查空间中线线垂直的证明和二面角的求解.
点评:在空间中证明直线、平面间的位置关系时,要紧扣判定定理和性质定理,定理中要求的条件要一一列举出来,缺一不可.

练习册系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.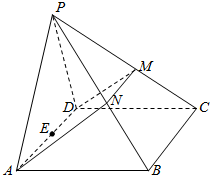 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥
如图,在四棱锥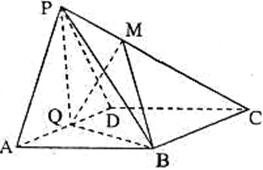 试确定
试确定