题目内容
 如图,在四棱锥
如图,在四棱锥![]() 中,侧面
中,侧面![]()
是正三角形,且与底面![]() 垂直,底面
垂直,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 是
是![]() 中点,过
中点,过![]() 、
、![]() 、
、![]() 三点的平面交
三点的平面交![]() 于
于![]() .
.
(1)求证:![]() ; (2)求证:
; (2)求证:![]() 是
是![]() 中点;(3)求证:平面
中点;(3)求证:平面![]() ⊥平面
⊥平面![]() .
.
(1)略 (2)略 (3)略
解析:
证明:(1)连结![]() ,
,![]() ,设
,设![]() ,连结
,连结![]()
∵![]() 是的菱形 ∴
是的菱形 ∴![]() 是
是![]() 中点,又
中点,又![]() 是
是![]() 中点,∴
中点,∴![]() , 又
, 又![]() , ∴
, ∴![]()
(2)依题意有![]() ∴
∴![]() 平面
平面![]() , 而平面
, 而平面![]() 平面
平面![]()
∴![]() , ∴
, ∴![]() ,(或证
,(或证![]() ∥平面
∥平面![]() ) ∴
) ∴![]()
又![]() 是
是![]() 中点 ∴
中点 ∴![]() 是
是![]() 中点
中点
(3)取AD中点E,连结![]() ,
,![]() ,
,![]() ,如右图
,如右图
∵![]() 为边长为2的菱形,且
为边长为2的菱形,且![]() ,∴
,∴![]() 为等边三角形,又
为等边三角形,又![]() 为
为![]() 的中点
的中点
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ⊥面
⊥面![]() ,∴AD⊥PB , 又∵
,∴AD⊥PB , 又∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() 平面
平面![]() 而
而![]() 平面
平面![]()
∴平面![]()
![]() 平面
平面![]()

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
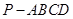 中,侧棱
中,侧棱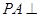 底面
底面 ,底面
,底面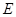 为
为 上一点,
上一点,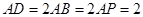 ,
,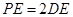 .
.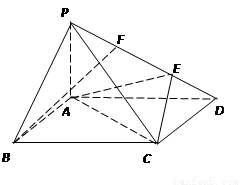
 为
为 的中点,求证
的中点,求证 平面
平面 ;
;  的体积.
的体积. 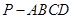 中,侧棱
中,侧棱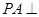 底面
底面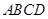 ,底面
,底面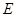 为
为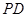 上一点,
上一点,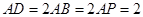 ,
,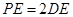 .
.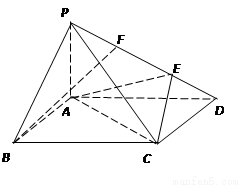
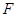 为
为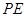 的中点,求证
的中点,求证 平面
平面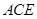 ;
; 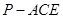 的体积.
的体积. 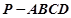 中,侧棱
中,侧棱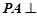 底面
底面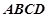 ,底面
,底面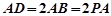 ,
,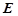 为
为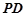 的上一点,且
的上一点,且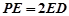 ,
,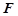 为PC的中点.
为PC的中点.

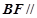 平面AEC;
平面AEC;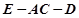 的余弦值.
的余弦值.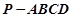 中,侧棱
中,侧棱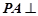 底面
底面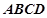 ,底面
,底面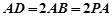 ,
, 为
为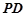 的上一点,且
的上一点,且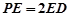 ,
,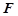 为PC的中点.
为PC的中点.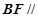 平面AEC;
平面AEC;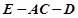 的余弦值.
的余弦值.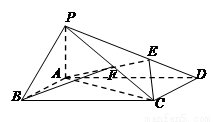
 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 ,
, 为
为 的上一点,且
的上一点,且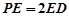 ,
, 为PC的中点.
为PC的中点. 平面AEC;
平面AEC; 的余弦值.
的余弦值.