题目内容
【题目】已知函数f（x）= 
，若关于x的方程f（f（x））=0有且只有一个实数解，则实数a的取值范围是（ ）
A.（﹣∞，0）
B.（﹣∞，0]∪（0，1）
C.（﹣∞，0）∪（0，1]
D.（﹣∞，0）∪（0，1）
【答案】D
【解析】解：令f（x）=t，方程f（f（x））=0有且只有一个实数解f（t）=0有且只有一个实数解． ①当a=0时．函数f（x）= 
的图象如图（1）；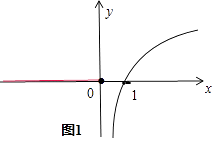
f（t）=0t=1或t≤0，即f（x）=t=1，或f（x）=t≤0，由无数个解，不符合题意．
②当a＞0时．函数f（x）= 的图象如图（2）；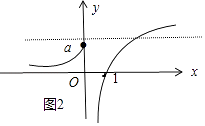
f（t）=0t=1，要使f（x）=t=1有且只有一个实数解，结合图象可得a＜1，
即0＜a＜1符合题意．
②当a＜0时．函数f（x）= 的图象如图（3）；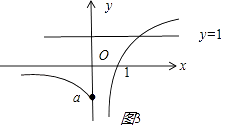
f（t）=0t=1，要使f（x）=t=1有且只有一个实数解，结合图象可得a＜0都成立．
综上实数a的取值范围是（0，1）∪（﹣∞，0），
故选：D．
练习册系列答案
相关题目
