题目内容
5.已知知函数f(x)=x3-ax2(其中a是实数),且f′(1)=0(1)求a的值及曲线y=f(x)在点(2,f(2))处的切线方程
(2)求f(x)≥kx-$\frac{1}{2}$在区间[0,2]上恒成立,求实数k的最大值.
分析 (1)求得导数,由条件可得a,求出切线的斜率和切点,由点斜式方程,可得切线的方程;
(2)由题意可得k≤$\frac{{x}^{3}-\frac{3}{2}{x}^{2}+\frac{1}{2}}{x}$=x2-$\frac{3}{2}$x+$\frac{1}{2x}$,令g(x)=x2-$\frac{3}{2}$x+$\frac{1}{2x}$,0<x≤2,运用导数,判断单调性,求得极小值,也为最小值,即可得到k的范围和最大值.
解答 解:(1)函数f(x)=x3-ax2的导数为f′(x)=3x2-2ax,
由f′(1)=0,可得a=$\frac{3}{2}$;
曲线y=f(x)在点(2,f(2))处的切线斜率为3×4-3×2=6,
切点为(2,2),
即有曲线y=f(x)在点(2,f(2))处的切线方程为y-2=6(x-2),
即为6x-y-10=0;
(2)f(x)≥kx-$\frac{1}{2}$在区间[0,2]上恒成立,
x=0时,f(0)=0>-$\frac{1}{2}$,显然成立;
即有k≤$\frac{{x}^{3}-\frac{3}{2}{x}^{2}+\frac{1}{2}}{x}$=x2-$\frac{3}{2}$x+$\frac{1}{2x}$,
令g(x)=x2-$\frac{3}{2}$x+$\frac{1}{2x}$,0<x≤2,
g′(x)=2x-$\frac{3}{2}$-$\frac{1}{2{x}^{2}}$=$\frac{4{x}^{3}-3{x}^{2}-1}{2{x}^{2}}$=$\frac{(x-1)(4{x}^{2}+x+1)}{2{x}^{2}}$,
由4x2+x+1>0恒成立,当0<x<1时,g′(x)<0,g(x)递减;
当1<x<2时,g′(x)>0,g(x)递增,
即有x=1处取得极小值,也为最小值0,
则有k≤0,
则有k的最大值为0.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用参数分离和构造函数求最值,属于中档题.

| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 合计 | 26 | 24 | 50 |
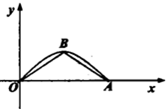 如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )
如图是函数f(x)=sinx(x∈[0,π])的图象,其中B为顶点,若在f(x)的图象与x轴所围成的区域内任意投进一个点P,则点P落在△OAB内的概率为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{{3}^{7}}{{2}^{8}}$ | B. | $\frac{{3}^{7}}{{2}^{9}}$ | C. | $\frac{{3}^{8}}{{2}^{8}}$ | D. | $\frac{{3}^{8}}{{2}^{9}}$ |