题目内容
已知函数![]()
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明:当![]()
答案:
解析:
解析:
|
解:(Ⅰ) 令 当x变化时,
所以f(x)的单调递增区间是(-∞,a-2),(a,+∞), 单调递减区间是(a-2,a) 6分 (Ⅱ)由(Ⅰ)得[f(x)]极大=f(a-2)=4ea-2. (1)当a≤1时,f(x)在(-∞,1]上的最大值为f(a-2)或f(1), 由 (2)当a-2≤1<a,即1<a≤3时,f(x)在(-∞,1]上的最大值为f(a-2), 此时f(a-2)=4ea-2≤4e3-2=4e; (3)当a-2>1,即a>3时,f(1)=(a-1)2e>4e,f(x)≤4e不恒成立. 综上,a的取值范围是[-1,3] 12分 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

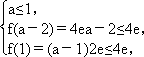 解得-1≤a≤1;
解得-1≤a≤1;
 ,求f(1)、f(-3)、f(a+1)的值.
,求f(1)、f(-3)、f(a+1)的值.