题目内容
已知函数![]() .
.
(1)求f(![]() )+f(-
)+f(-![]() )的值;
)的值;
(2)当x∈![]() (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时,
f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由.
(1)0,(2)当x∈![]() (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时,
f(x)存在最小值,,且最小值为f(a)= -a+log2![]()
解析:
(1)f(x)的定义域是(-1, 1),
∵f(-x)=-(-x) +log2![]() =-(-x+log2
=-(-x+log2![]() )=- f(x)
)=- f(x)
∴f(x)为奇函数. ∴f(![]() )+f(-
)+f(-![]() )=0. ……5分
)=0. ……5分
(直接运算也可以)
(2)设-1< x1< x2 <1,
∵f(x2)-f(x1)= - x2+ log2![]() -[- x1+ log2
-[- x1+ log2![]() ] ……7分
] ……7分
=( x1- x2)+ log2![]() ,
,
∵x1- x2< 0, 1+x1-x2- x1x2-(1+x2-x1- x1x2)=2(x1- x2)<0,
∴1+x1-x2- x1x2< 1+x2-x1- x1x2.
∴0<![]() <1.
<1.
∴log2![]() < 0.
< 0.
∴f(x2)-f(x1) < 0. ∴f(x)在(-1, 1)上单调递减. ……10分
∴当x∈![]() (其中a∈(0, 1), 且a为常数)时,
(其中a∈(0, 1), 且a为常数)时,
f(x)存在最小值,,且最小值为f(a)= -a+log2![]() ……12分
……12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,
,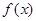 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
,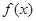 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.