Question

5．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F₂，M（x₀，y₀）（x₀＞0，y₀＞0）是双曲线C上的点，N（-x₀，-y₀），连接MF₂并延长MF₂交双曲线C于P，连接NF₂，PN，若△NF₂P是以∠NF₂P为顶角的等腰直角三角形，则双曲线C的渐近线方程为（　　）

• A． y=±2x
• B． y=±4x
• C． y=±$\frac{\sqrt{6}}{2}$x
• D． y=±$\frac{\sqrt{10}}{2}$x

Answer 1

分析 可设双曲线的左焦点为F₁，并连接MF₁，MF₂，根据双曲线的对称性及条件便知四边形F₁NF₂M为矩形，可设MF₂=x，并连接PF₁，这样根据双曲线的定义及平行四边形对边相等即可得出MF₁=2a+x，MP=2a+2x，PF₁=4a+x，这样根据直角三角形的边的关系即可得到$\left\{\begin{array}{l}{（2a+x）^{2}+{x}^{2}=4{c}^{2}}&{①}\\{（2a+x）^{2}+（2a+2x）^{2}=（4a+x）^{2}}&{②}\end{array}\right.$，这样可以由②解出x，带入①中便可得到a，b，c的关系，根据c²=a²+b²即可得出$\frac{b}{a}$的值，从而便得出渐近线方程．

解答 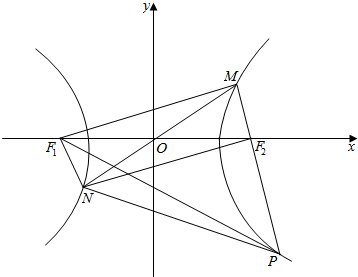解：如图，设F₁为双曲线左焦点，连接MF₁，NF₁，则：
由对称性可知四边形F₁NF₂M为平行四边形；
又∠MF₂N=90°；
∴F₁NF₂M为矩形；
设MF₂=x，则MF₁=2a+x；
∴PF₂=NF₂=MF₁=2a+x；
∴PF₁=2a+PF₂=4a+x；
在Rt△MF₁F₂中有：（2a+x）²+x²=4c² ①；
在Rt△MF₁P中有：（2a+x）²+（2a+2x）²=（4a+x）² ②；
由②解得，x=a，代回①得：9a²+a²=4c²；
∴${c}^{2}=\frac{5}{2}{a}^{2}$；
∴${b}^{2}={c}^{2}-{a}^{2}=\frac{3}{2}{a}^{2}$；
∴$\frac{b}{a}=\frac{\sqrt{6}}{2}$；
∴渐近线方程为：y=$±\frac{b}{a}x=±\frac{\sqrt{6}}{2}x$．
故选C．

点评 考查双曲线的对称性，双曲线的标准方程，双曲线的焦点，以及双曲线的定义，直角三角形的边的关系，c²=a²+b²，双曲线的渐近线方程．