题目内容
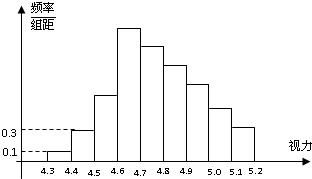 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.7到4.8之间的学生数为( )
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.7到4.8之间的学生数为( )分析:由题意可得前4组的频数分别为1,3,9,27.再根据总共有9组,设后6组的频数分别为27、27+d、27+2d、27+3d、27+4d、27+5d,再由各组的频数之和等于100,解得d的值,可得各组的频数,从而得到答案.
解答:解:由频率分布直方图可得前2组的频率分别为0.01、0.03,故前2组的频数分别为1、3,
再根据前4组的频数成等比数列,可得前4组的频数分别为1,3,9,27.
再根据总共有9组,后6组的频数成等差数列,可得后6组的频数分别为27、27+d、27+2d、
27+3d、27+4d、27+5d,
再由1+3+9+27+(27+d)+(27+2d)+(27+3d )+(27+4d)+(27+5d)=100,
解得 d=-5,
故各组的频数分别为1、3、9、27、22、17、12、7、2,
则视力在4.7到4.8之间的数据位于第5组,频数为22,
则视力在4.7到4.8之间的学生数为22,
故选C.
再根据前4组的频数成等比数列,可得前4组的频数分别为1,3,9,27.
再根据总共有9组,后6组的频数成等差数列,可得后6组的频数分别为27、27+d、27+2d、
27+3d、27+4d、27+5d,
再由1+3+9+27+(27+d)+(27+2d)+(27+3d )+(27+4d)+(27+5d)=100,
解得 d=-5,
故各组的频数分别为1、3、9、27、22、17、12、7、2,
则视力在4.7到4.8之间的数据位于第5组,频数为22,
则视力在4.7到4.8之间的学生数为22,
故选C.
点评:本题主要考查频率分布直方图,等差数列的定义、通项公式、前n项和公式的应用,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
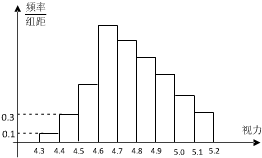 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a+b的值为
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a+b的值为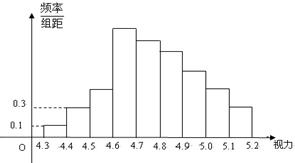 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图所示;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列{an}的前四项,后6组的频数从左到右依次是等差数列{bn}的前六项.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图所示;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列{an}的前四项,后6组的频数从左到右依次是等差数列{bn}的前六项. 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎,部分数据丢失,但知道前四组的频数成等比数列,后六组的频数成等差数列,设最大频率为a,视 力在4.6到5.0之间的学生数为b,则a+b的值为
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎,部分数据丢失,但知道前四组的频数成等比数列,后六组的频数成等差数列,设最大频率为a,视 力在4.6到5.0之间的学生数为b,则a+b的值为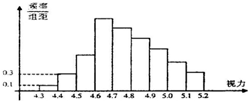 (2009•淄博一模)为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数b,则a、b的值分别为( )
(2009•淄博一模)为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数b,则a、b的值分别为( ) (2012•黄州区模拟)为了解某校高三学生的视力情况,随机地抽查了该校100名学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,只知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.1之间的学生人数为b,则a和b的值分别为( )
(2012•黄州区模拟)为了解某校高三学生的视力情况,随机地抽查了该校100名学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,只知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.1之间的学生人数为b,则a和b的值分别为( )