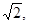题目内容
锐角△ABC中,若A=2B,则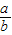 的取值范围是( )
的取值范围是( )A.(1,2)
B.(1,
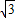 )
)C.(
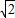 ,2)
,2)D.(
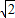 ,
,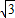 )
)
【答案】分析:利用题意可求得B的范围,进而利用正弦定理把边的比转化成角的正弦的比,利用二倍角公式整理求得sinA和sinB的关系,答案可得.
解答:解:∵△ABC为锐角三角形,且A=2B,
∴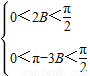 ,
,
∴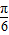 <B<
<B<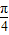 ,
,
∴sinA=sin2B=2sinBcosB,
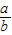 =
=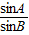 =2cosB∈(
=2cosB∈(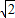 ,
,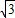 ).
).
故选D
点评:本题主要考查了正弦定理的应用.关键是就是边的问题转化成角的问题来解决.
解答:解:∵△ABC为锐角三角形,且A=2B,
∴
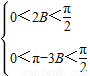 ,
,∴
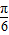 <B<
<B<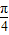 ,
,∴sinA=sin2B=2sinBcosB,
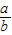 =
=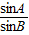 =2cosB∈(
=2cosB∈(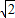 ,
,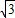 ).
).故选D
点评:本题主要考查了正弦定理的应用.关键是就是边的问题转化成角的问题来解决.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
锐角△ABC中,若A=2B,则
的取值范围是( )
| a |
| b |
| A、(1,2) | ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
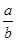 的取值范围是 ( )
的取值范围是 ( )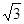 ) C.(
) C.(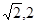 ) D.(
) D.(