题目内容
锐角△ABC中,若A=2B,则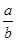 的取值范围是 ( )
的取值范围是 ( )
A.(1,2) B.(1,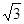 ) C.(
) C.(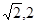 ) D.(
) D.(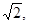
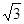 )
)
【答案】
D
【解析】
试题分析:利用题意可求得B的范围,进而利用正弦定理把边的比转化成角的正弦的比,利用二倍角公式整理求得sinA和sinB的关系,答案可得.:∵△ABC为锐角三角形,且A=2B,
∴0<2B<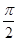 ,0<π-3B<
,0<π-3B<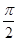 ,∴
,∴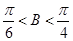 ,∴sinA=sin2B=2sinBcosB,借助于正弦定理可知,
,∴sinA=sin2B=2sinBcosB,借助于正弦定理可知,
asinB=bsinA, 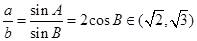 ,故选D.
,故选D.
考点:本题主要考查正弦定理的应用.
点评:解决该试题的关键是就是边的问题转化成角的问题来解决.注意借助于二倍角公式来化简求解范围。

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
锐角△ABC中,若A=2B,则
的取值范围是( )
| a |
| b |
| A、(1,2) | ||||
B、(1,
| ||||
C、(
| ||||
D、(
|