题目内容
如图,直三棱柱ABC-A1B1C1中,底面是以B为直角顶点的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,F在线段AA1上,
(Ⅰ)AF为何值时,CF⊥平面B1DF?
(Ⅱ)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值。
(Ⅰ)AF为何值时,CF⊥平面B1DF?
(Ⅱ)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值。
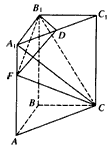
| 解:(Ⅰ)因为直三棱柱ABC-A1B1C1中, BB1⊥面ABC,∠ABC= 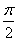 , ,以B点为原点,BA,BC,BB1分别为x,y,z轴 建立如图所示空间直角坐标系, 因为AC=2,∠ABC=90°,所以 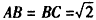 , ,从而 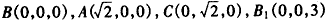 , , , ,所以 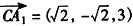 , ,设AF=x,则 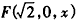 , ,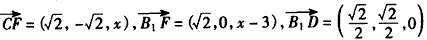 , ,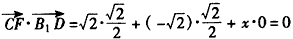 , ,所以 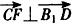 , ,要使CF⊥平面B1DF,只需CF⊥B1F, 由 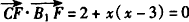 ,得x=1或x=2, ,得x=1或x=2,故当AF=1或2时,CF⊥平面B1DF。 (Ⅱ)由(Ⅰ)知平面ABC的法向量为 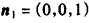 , ,设平面B1CF的法向量为n=(x,y,z), 则由 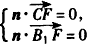 ,得 ,得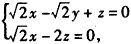 , ,令z=1得 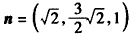 , ,所以平面B1CF与平面ABC所成的锐二面角的余弦值 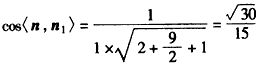 。 。 |
 |

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.