题目内容
设椭圆 的左、右焦点分别为
的左、右焦点分别为 ,,右顶点为A,上顶点为B.已知
,,右顶点为A,上顶点为B.已知 =
=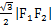 .
.
(1)求椭圆的离心率;
(2)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点 ,经过点
,经过点 的直线
的直线 与该圆相切与点M,
与该圆相切与点M, =
= .求椭圆的方程.
.求椭圆的方程.
 的左、右焦点分别为
的左、右焦点分别为 ,,右顶点为A,上顶点为B.已知
,,右顶点为A,上顶点为B.已知 =
=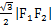 .
.(1)求椭圆的离心率;
(2)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点
 ,经过点
,经过点 的直线
的直线 与该圆相切与点M,
与该圆相切与点M, =
= .求椭圆的方程.
.求椭圆的方程.(1) 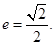 (2)
(2) 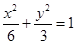
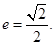 (2)
(2) 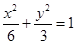
试题分析:(1)求椭圆离心率,就是列出关于a,b,c的一个等量关系.由
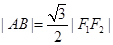 ,可得
,可得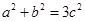 ,又
,又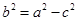 ,则
,则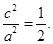 所以椭圆离心率为
所以椭圆离心率为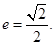 (2) 由(1)知
(2) 由(1)知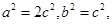 所以求椭圆方程只需再确定一个独立条件即可.由切线长
所以求椭圆方程只需再确定一个独立条件即可.由切线长 =
= 可列出所需的等量关系.先确定圆心:设
可列出所需的等量关系.先确定圆心:设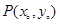 ,由
,由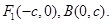 ,有
,有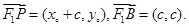 由已知,有
由已知,有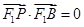 即
即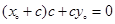 ,故有
,故有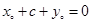 ,因为点P在椭圆上,故
,因为点P在椭圆上,故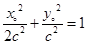 ,消
,消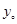 可得
可得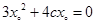 ,而点P不是椭圆的顶点,故
,而点P不是椭圆的顶点,故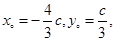 ,即点P的坐标为
,即点P的坐标为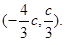 设圆的圆心为
设圆的圆心为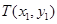 ,则
,则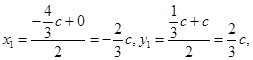 再由
再由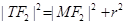 得
得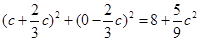 ,即
,即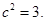 所以所求椭圆的方程为
所以所求椭圆的方程为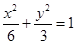
试题解析:解(1)设椭圆右焦点
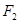 的坐标为(c,0), 由
的坐标为(c,0), 由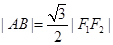 ,可得
,可得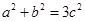 ,又
,又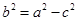 ,则
,则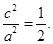 所以椭圆离心率为
所以椭圆离心率为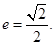 (2)由(1)知
(2)由(1)知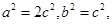 故椭圆方程为
故椭圆方程为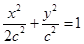 ,设
,设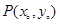 ,由
,由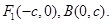 ,有
,有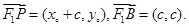 由已知,有
由已知,有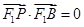 即
即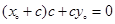 ,故有
,故有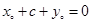 ,因为点P在椭圆上,故
,因为点P在椭圆上,故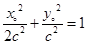 ,消
,消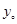 可得
可得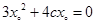 ,而点P不是椭圆的顶点,故
,而点P不是椭圆的顶点,故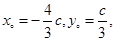 ,即点P的坐标为
,即点P的坐标为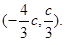 设圆的圆心为
设圆的圆心为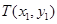 ,则
,则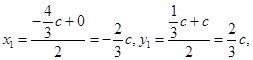 ,进而圆的半径
,进而圆的半径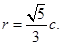 ,由已知,有
,由已知,有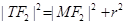 ,
, =
= ,故有
,故有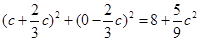 ,解得
,解得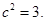 ,所以所求椭圆的方程为
,所以所求椭圆的方程为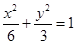

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
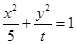 恒有公共点,则t的取值范围是 .
恒有公共点,则t的取值范围是 .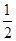
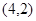 是直线
是直线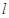 被椭圆
被椭圆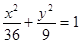 所截得的线段的中点,则直线
所截得的线段的中点,则直线



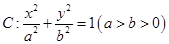 的一个焦点为
的一个焦点为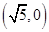 ,离心率为
,离心率为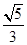 .
.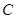 的标准方程;
的标准方程;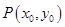 为椭圆
为椭圆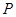 到椭圆
到椭圆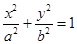 (
(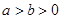 )的左、右焦点为
)的左、右焦点为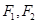 ,右顶点为
,右顶点为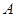 ,上顶点为
,上顶点为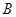 .已知
.已知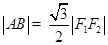 .
.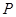 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段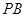 为直径的圆经过点
为直径的圆经过点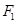 ,经过原点
,经过原点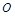 的直线
的直线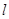 与该圆相切,求直线
与该圆相切,求直线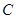 :
: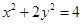 .
.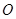 为原点,若点
为原点,若点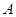 在椭圆
在椭圆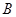 在直线
在直线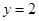 上,且
上,且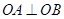 ,试判断直线
,试判断直线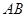 与圆
与圆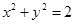 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.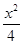 +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )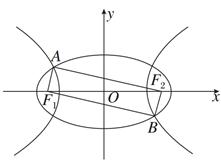

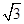


 +y2=1的焦点,点A,B在椭圆上,若
+y2=1的焦点,点A,B在椭圆上,若 =5
=5 ;则点A的坐标是 _________ .
;则点A的坐标是 _________ .