题目内容
6．（1）已知a，b∈R，求证2（a2+b2）≥（a+b）2．（2）已知x∈R，a=x2-1，b=2x+2，求证a，b中至少有一个不小于0．
分析 （1）直接利用分析法、综合法的证明步骤证明即可；
（2）假设a＜0，b＜0，则a+b＜0，又a+b=x2-1+2x+2=x2+2x+1=（x+1）2≥0，这与假设所得结论矛盾，故假设不成立．
解答 证明：（1）证法1：要证2（a2+b2）≥（a+b）2，
只要证2a2+2b2≥a2+2ab+b2，
只要证a2+b2≥2ab，
而a2+b2≥2ab显然成立，
所以2（a2+b2）≥（a+b）2成立．
证法2：因为2（a2+b2）-（a+b）2
=2a2+2b2-（a2+2ab+b2）
=a2+b2-2ab
=（a-b）2≥0，
所以2（a2+b2）≥（a+b）2．
（2）假设a，b都小于0，即a＜0，b＜0，
所以a+b＜0，
又a+b=x2-1+2x+2=x2+2x+1=（x+1）2≥0，
这与假设所得结论矛盾，故假设不成立．
所以a，b中至少有一个不小于0．
点评 本题考查分析法的证明方法，考查用反证法证明数学命题，推出矛盾是解题的关键，考查逻辑推理能力．
练习册系列答案
相关题目
16．运行如图所示的程序框图，则输出k的值是（ ）
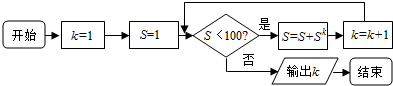
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
如图，在三棱锥P-ABC中，AB⊥AC，PA=PB=PC=3，AB=2$\sqrt{3}$，AC=2，