题目内容
若函数 的图像与
的图像与 轴有公共点,则
轴有公共点,则 的取值范围是( )
的取值范围是( )
A. B.
B.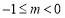 C.
C. D.
D.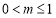
B
【解析】
试题分析:函数与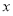 轴有公共点,即设函数
轴有公共点,即设函数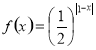 ,
,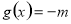 ,有交点,函数
,有交点,函数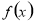 如图:
如图:
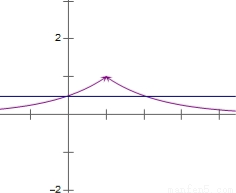
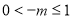 ,即
,即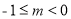 ,故选B.
,故选B.
考点:函数图像

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
题目内容
若函数 的图像与
的图像与 轴有公共点,则
轴有公共点,则 的取值范围是( )
的取值范围是( )
A. B.
B.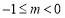 C.
C. D.
D.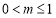
B
【解析】
试题分析:函数与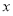 轴有公共点,即设函数
轴有公共点,即设函数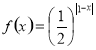 ,
,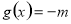 ,有交点,函数
,有交点,函数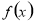 如图:
如图:

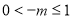 ,即
,即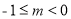 ,故选B.
,故选B.
考点:函数图像

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案