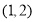题目内容
如图所示,圆锥的轴截面为等腰直角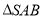 ,
,  为底面圆周上一点.
为底面圆周上一点.

(1)若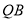 的中点为
的中点为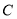 ,
,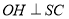 ,求证
,求证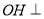 平面
平面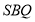 ;
;
(2)如果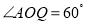 ,
, ,求此圆锥的全面积.
,求此圆锥的全面积.
(1)详见解析;(2)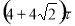 .
.
【解析】
试题分析:(1)要证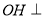 平面
平面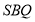 ,即证
,即证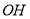 垂直于平面内的两条相交直线,
垂直于平面内的两条相交直线, 是已知,转化为证
是已知,转化为证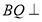 平面
平面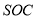 ,利用母线相等,利用底面半径相等,
,利用母线相等,利用底面半径相等,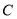 为中点,证得
为中点,证得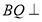 平面
平面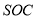 ,证得,
,证得,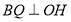 ,得证;(2)
,得证;(2)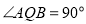 ,求出底面半径,以及母线长,根据全面积公式,
,求出底面半径,以及母线长,根据全面积公式,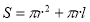 ,求出全面积.
,求出全面积.
试题解析:【解析】
①连接OC,
∵OQ=OB,C为QB的中点,∴OC⊥QB 2分
∵SO⊥平面ABQ,BQ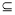 平面ABQ
平面ABQ
∴SO⊥BQ,结合SO∩OC=0,可得BQ⊥平面SOC
∵OH?平面SOC,∴BQ⊥OH, 5分
∵OH⊥SC,SC、BQ是平面SBQ内的相交直线,
∴OH⊥平面SBQ; 6分
②∵∠AOQ=60°,QB=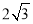 ,∴直角△ABQ中,∠ABQ=30°,
,∴直角△ABQ中,∠ABQ=30°,
可得AB=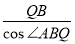 =4 8分
=4 8分
∵圆锥的轴截面为等腰直角△SAB,
∴圆锥的底面半径为2,高SO=2,可得母线SA=2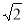 ,
,
因此,圆锥的侧面积为S侧=π×2×2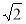 =4
=4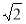 π 10分
π 10分
∴此圆锥的全面积为S侧+S底=4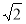 π+π×22=(4+4
π+π×22=(4+4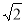 )π 12分
)π 12分
考点:1.线面垂直的判定;2.线面垂直的性质;3.几何体的表面积.

练习册系列答案
相关题目