题目内容
已知函数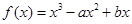 的图象为曲线E.
的图象为曲线E.
(1)若a = 3,b = -9,求函数f(x)的极值;
(2)若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系.
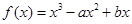 的图象为曲线E.
的图象为曲线E.(1)若a = 3,b = -9,求函数f(x)的极值;
(2)若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系.
(1)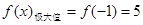 ,
,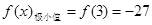 ;(2)
;(2)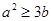 .
.
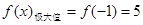 ,
,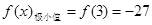 ;(2)
;(2)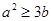 .
.试题分析:(1)欲求函数极值应先求函数导数,并求出
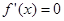 的根,再判断在根左右导数是否异号,若成立则此根为极值点,代入函数解析式可求极值.(2)对于存在性问题,一般假设存在然后依条件求出,若有则有,若无则假设不成立.
的根,再判断在根左右导数是否异号,若成立则此根为极值点,代入函数解析式可求极值.(2)对于存在性问题,一般假设存在然后依条件求出,若有则有,若无则假设不成立.试题解析:
(1)当
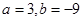 时,
时,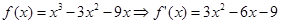 .令
.令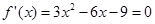 ,可得
,可得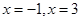 .
.| 区间 | 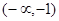 | 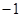 | 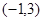 |  | 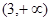 |
 | + | 0 | - | 0 | + |
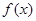 | 递增 | 极大值 | 递减 | 极小值 | 递增 |
当
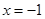 时,
时,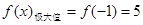 ,当
,当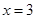 时,
时,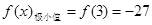 5分
5分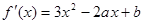 ,设切点为
,设切点为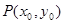 ,
,则曲线
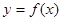 在点P的切线的斜率
在点P的切线的斜率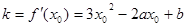
由题意知
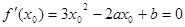 有解
有解∴
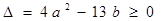 即
即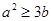 . 10分
. 10分
练习册系列答案
相关题目
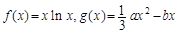 ,其中a,b∈R
,其中a,b∈R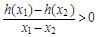 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;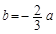 时,若
时,若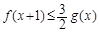 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.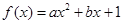 (
(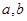 为实数,
为实数,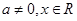 ),
),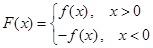 ,⑴若
,⑴若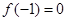 ,且函数
,且函数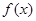 的值域为
的值域为 ,求
,求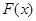 的表达式;
的表达式;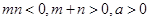 ,且函数
,且函数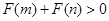 是否大0?
是否大0?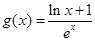 ,当
,当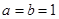 时,证明:对任意实数
时,证明:对任意实数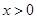 ,
,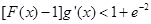 (其中
(其中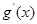 是
是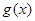 的导函数) .
的导函数) .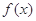 定义在
定义在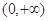 上的非负可导函数,且满足
上的非负可导函数,且满足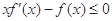 ,对任意正数
,对任意正数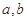 , 若
, 若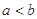 ,则必有( ).
,则必有( ).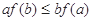



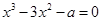 有三个不同的实数解,则a的取值范围是__________.
有三个不同的实数解,则a的取值范围是__________.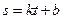 表示,则该匀速运动的平均速度与任何时刻的瞬时速度( )
表示,则该匀速运动的平均速度与任何时刻的瞬时速度( )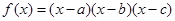 ,(
,(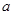 、
、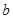 、
、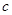 是两两不等的常数),则
是两两不等的常数),则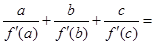 .
.