题目内容
设P是△ABC内一点，△ABC三边上的高分别为hA、hB、hC，P到三边的距离依次为la、lb、lc，则有
+
+
=1；类比到空间，设P是四面体ABCD内一点，四顶点到对面的距离分别是hA、hB、hC、hD，P到这四个面的距离依次是la、lb、lc、ld，则有
+
+
+
=1
+
+
+
=1．
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
分析：在平面中利用面积分割法，结合三角形面积公式证出
+
+
=1，结论成立．依此可得当P为四面体ABCD内一点时，利用体积分割法和锥体的体积公式，类似于平面中结论的证明方法可得
+
+
+
=1，得到本题答案．
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
解答：解：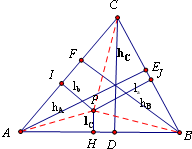
如图，连结PA、PB、PC，可得
S△ABP+S△BCP+S△CAP=S△ABC，
即
AB×lc+
BC×la+
CA×lb=S△ABC，…（1）
∵S△ABC=
AB×hC=
BC×hA=
CA×hB
∴在（1）式的两边都除以S△ABC，得
+
+
=1
即
+
+
=1，即平面内的结论成立
当P为四面体ABCD内一点时，VP-BCD+VP-CDA+VP-ABD+VP-ABC=VD-ABC，
两边都除以VD-ABC，得
+
+
+
=1
类似平面中结论证明的方法，可得
+
+
+
=1
故答案为：
+
+
+
=1
如图，连结PA、PB、PC，可得S△ABP+S△BCP+S△CAP=S△ABC，
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴在（1）式的两边都除以S△ABC，得
| lc |
| h C |
| la |
| h A |
| lb |
| h B |
即
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
当P为四面体ABCD内一点时，VP-BCD+VP-CDA+VP-ABD+VP-ABC=VD-ABC，
两边都除以VD-ABC，得
| VP-BCD |
| VD-ABC |
| VP-CDA |
| VD-ABC |
| VP-ABD |
| VD-ABC |
| VP-ABC |
| VD-ABC |
类似平面中结论证明的方法，可得
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
故答案为：
| la |
| hA |
| lb |
| hB |
| lc |
| hC |
| ld |
| hD |
点评：本题给出三角形ABC内一点P满足的等式，要求给出空间四面体的一个类似结论．着重考查了三角形面积公式、锥体的体积公式和类比推理的一般方法等知识，属于中档题．
练习册系列答案
相关题目
=______________；类比到空间，设P为四面体ABCD内一点，四个顶点到对面的距离分别是hA,hB,hC,hD，P到这四个面的距离依次是lA,lB,lC,lD，则有______________.
+
+
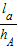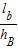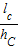=1；类比到空间，设P是四面体ABCD内一点，四顶点到对面的距离分别是hA、hB、hC、hD，P到这四个面的距离依次是la、lb、lc、ld，则有 ．
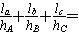（ ）；类比到空间，设P为四面体ABCD内一点，四个顶点到对面的距离分别是hA、hB、hC、hD，P 到这四个面的距离依次是la、lb、lc、ld，则有（ ）。