题目内容
【题目】已知函数f(x)=1﹣ ![]() (a>0且a≠1)是定义在R上的奇函数.
(a>0且a≠1)是定义在R上的奇函数.
(1)求a的值;
(2)求f(x)的值域;
(3)若关于x的方程|f(x)(2x+1)|=m有1个实根,求实数m的取值范围;
(4)当x∈(0,1]时,tf(x)≥2x﹣2恒成立,求实数t取值范围.
【答案】
(1)解:∵函数f(x)=1﹣ ![]() (a>0且a≠1)是定义在R上的奇函数,
(a>0且a≠1)是定义在R上的奇函数,
∴f(﹣x)=﹣f(x),解得:a=2
(2)解: ![]() ,
,
∴y∈(﹣1,1)
(3)解:设h(x)=|2x﹣1|,g(x)=m,
作图,如图示:
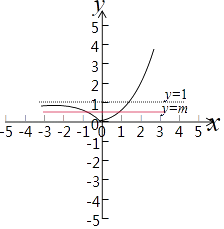
如图当m≥1时,h(x)=|2x﹣1|与g(x)=m有一个交点,
所以|f(x)(2x+1)|=m有一个实根,
所以m∈[1,+∞)∪{0}
(4)解: ![]() (2x)2﹣(t+1)2x+t﹣2≤0,
(2x)2﹣(t+1)2x+t﹣2≤0,
令2x=u,x∈(0,1]u∈(1,2],
u∈(1,2]时,u2﹣(t+1)u+t﹣2≤0恒成立,
则 ![]()
【解析】(1)根据函数的奇偶性得到f(﹣x)=﹣f(x),求出a的值即可;(2)将f(x)变形,解关于y的不等式,求出f(x)的值域即可;(3)结合图象求出m的范围即可;(4)令2x=u,x∈(0,1]u∈(1,2],得到u∈(1,2]时,u2﹣(t+1)u+t﹣2≤0恒成立,求出t的范围即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目