题目内容

已知抛物线C的方程为，焦点为F，有一定点，A在抛物线准线上的射影为H，P为抛物线上一动点.

（1）当|AP|+|PF|取最小值时，求；

 

（2）如果一椭圆E以O、F为焦点，且过点A，求椭圆E的方程及右准线方程；

（3）设是过点A且垂直于x轴的直线，是否存在直线，使得与抛物线C交于两个

不同的点M、N，且MN恰被平分？若存在，求出的倾斜角的范围；若不存在，请

说明理由.

 

【答案】

解：（1）由定义知，当P为AH与抛物线的交点时，|PF|=|PH|

此时|AP|+|PF|=|AH|取得最小值4………………4分

得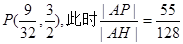………………6分

（2）由（1）知，椭圆E的焦点为O（0，0），F（2，0）

故中心为（1，0）.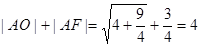

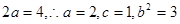
所求椭圆方程为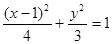………………8分

右准线方程为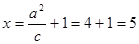………………10分

（3）由条件知，过A且与x轴垂直的直线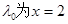

设满足条件的直线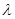存在，并设其方程为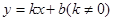

代入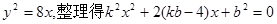………………①

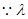与C交于不同的两点M、N，故方程①的

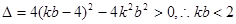………………12分

设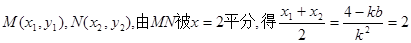

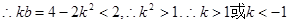
故直线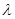存在，其倾斜角的取值范围为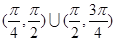…………14分

【解析】略

 

练习册系列答案
相关题目
已知抛物线C的方程为y=x2，过（0，1）点的直线l与C相交于点A，B，证明：OA⊥OB（O为坐标原点）
（2013•浙江模拟）已知抛物线C的方程为y2=2px（p＞0），直线：x+y=m与x轴的交点在抛物线C准线的右侧．
（Ⅰ）求证：直线与抛物线C恒有两个不同交点；
（Ⅱ）已知定点A（1，0），若直线与抛物线C的交点为Q，R，满足
AQ
•
AR
=0，是否存在实数m，使得原点O到直线的距离不大于
2
4
，若存在，求出正实数p的取值范围；若不存在，请说明理由．
（2011•合肥三模）已知抛物线C的方程为x2=2py（p＞0），过抛物线上点M（-2
p
，p）作△MAB，A、B两均在抛物线上．过M作x轴的平行线，交抛物线于点N．
（I）若MN平分∠AMB，求证：直线AB的斜率为定值；
（II）若直线AB的斜率为
p
，且点N到直线MA，MB的距离的和为4p，试判断△MAB的形状，并证明你的结论．
已知抛物线C的方程为x2=2py（p＞0），焦点F为 （0，1），点P（x1，y1）是抛物线上的任意一点，过点P作抛物线的切线交抛物线的准线l于点A（s，t）．
（1）求抛物线C的标准方程；
（2）若x1∈[1，4]，求s的取值范围．
（3）过点A作抛物线C的另一条切线AQ，其中Q（x2，y2）为切点，试问直线PQ是否恒过定点，若是，求出定点；若不是，请说明理由．
已知抛物线C的方程为y2=2px（p＞0且p为常数），过焦点F作直线与抛物线交于A（x1，y1），B（x2，y2）
①求证：4x1x2=p2
②若抛物线C的准线l与x轴交于N点且AB⊥AN，求|x1-x2|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网