题目内容
已知抛物线C的方程为y2=2px(p>0且p为常数),过焦点F作直线与抛物线交于A(x1,y1),B(x2,y2)
①求证:4x1x2=p2
②若抛物线C的准线l与x轴交于N点且AB⊥AN,求|x1-x2|
①求证:4x1x2=p2
②若抛物线C的准线l与x轴交于N点且AB⊥AN,求|x1-x2|
分析:(1)结合要证明的结果可联想到将A,B所在得直线方程与抛物线C的方程为y2=2px(p>0且p为常数)联立然后利用根与系数的关系即可得证,而根据题意F(
,0)故可利用点斜式写出直线AB的方程但要分斜率存在与否进行讨论.
(2)根据题意易得N(-
,0)再根据AB⊥AN可得kAB•kAN=-1再结合y12=2px1以及第一问的结论4x1x2=p2,化简即可得解.
| p |
| 2 |
(2)根据题意易得N(-
| p |
| 2 |
解答:解: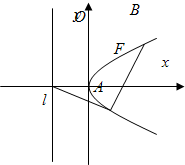 (1)设直线AB的方程为y=k(x-
(1)设直线AB的方程为y=k(x-
)(k≠0)
(当 k=0时,显然不合题意)
联立
⇒k2x2-(k2p+2p)x+
=0
由韦达定理得:x1x2=
,即4x1x2=p2
当AB的斜率k不存在时,AB的方程为x=
此时x1=x2=
,4x1x2=p2也成立.
(2)抛物线y2=2px的准线方程为x=-
,准线与x轴交点N(-
,0),A(x1,y1)(显然x1≠0)kAN=
,kAB=kAF=
∵AB⊥AN∴
•
=-1得y12=
-x12
但y12=2px1由①知:
=x1x2,故有2px1=x1x2-x12
又x1≠0∴2p=x2-x1即有:|x2-x1|=2p
 (1)设直线AB的方程为y=k(x-
(1)设直线AB的方程为y=k(x-| p |
| 2 |
(当 k=0时,显然不合题意)
联立
|
| k2p2 |
| 4 |
由韦达定理得:x1x2=
| p2 |
| 4 |
当AB的斜率k不存在时,AB的方程为x=
| p |
| 2 |
此时x1=x2=
| p |
| 2 |
(2)抛物线y2=2px的准线方程为x=-
| p |
| 2 |
| p |
| 2 |
| y1 | ||
x1+
|
| y1 | ||
x1-
|
| y1 | ||
x1+
|
| y1 | ||
x1-
|
| p2 |
| 4 |
但y12=2px1由①知:
| p2 |
| 4 |
又x1≠0∴2p=x2-x1即有:|x2-x1|=2p
点评:本题主要是对直线与圆锥曲线的综合问题的考查.解题的关键是第一问要对直线的斜率存在与否进行讨论而第二问要对AB⊥AN这一条件的常用运算技巧熟悉(即kAB•kAN=-1)在得出y12=
-x12后结合要求的结果|x1-x2|故需利用点A在抛物线上以及第一问的结论再对上式代入化简求值!
| p2 |
| 4 |

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 (2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2
(2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2 已知抛物线C的方程为x2=2py(p>0),焦点F为 (0,1),点P(x1,y1)是抛物线上的任意一点,过点P作抛物线的切线交抛物线的准线l于点A(s,t).
已知抛物线C的方程为x2=2py(p>0),焦点F为 (0,1),点P(x1,y1)是抛物线上的任意一点,过点P作抛物线的切线交抛物线的准线l于点A(s,t).