题目内容
7.解下列方程:(1)$\frac{[x]}{x}$=$\frac{x}{[x]}$,x>0;
(2)[3x+1]=2x-$\frac{1}{2}$;
(3)x2-8[x]+7=0;
(4)[x]+[2x]=18.
分析 (1)由$\frac{[x]}{x}$=$\frac{x}{[x]}$,x>0,化为[x]=x,即可解出;
(2)[3x+1]=2x-$\frac{1}{2}$,化为[3x]+1=2x-$\frac{1}{2}$,[3x]=2x-$\frac{3}{2}$≤3x,解得x≥$-\frac{3}{2}$.记[3x]=2x-$\frac{3}{2}$(*).分类讨论:当-$\frac{3}{2}$≤x<-$\frac{4}{3}$时;当-$\frac{4}{3}$≤x<-1时;当-1≤x<-$\frac{2}{3}$时,当-$\frac{2}{3}$≤x<-$\frac{1}{3}$时,当$-\frac{1}{3}$≤x<0时,当x∈$[\frac{n}{3},\frac{n+1}{3})$时(n∈N),即可得出;
(3)x2-8[x]+7=0化为x2+7=8[x]≤8x,解得1≤x≤7.化为[x]=$\frac{1}{8}({x}^{2}+7)$,分类讨论:当x∈[1,2)时,当x∈[3,4)时,…,当x∈[6,7)时,当x=7时,解出即可.
(4)由于2[x]≤[2x]≤2[x]+1,可得$\frac{17}{3}$≤[x]≤6,解出并验证即可得出.
解答 解:(1)$\frac{[x]}{x}$=$\frac{x}{[x]}$,x>0,∴[x]=x,∴x=n∈N*;
(2)[3x+1]=2x-$\frac{1}{2}$,化为[3x]+1=2x-$\frac{1}{2}$,∴[3x]=2x-$\frac{3}{2}$≤3x,解得x≥$-\frac{3}{2}$.
记[3x]=2x-$\frac{3}{2}$(*).
当-$\frac{3}{2}$≤x<-$\frac{4}{3}$时,(*)化为:-5=2x-$\frac{3}{2}$,解得x=-$\frac{7}{4}$,不满足条件,舍去;
当-$\frac{4}{3}$≤x<-1时,(*)化为:-4=2x-$\frac{3}{2}$,解得x=-$\frac{5}{4}$,满足条件,因此x=-$\frac{5}{4}$为方程的一个解;
当-1≤x<-$\frac{2}{3}$时,(*)化为:-3=2x-$\frac{3}{2}$,解得x=-$\frac{3}{4}$,满足条件,因此x=-$\frac{3}{4}$为方程的一个解;
当-$\frac{2}{3}$≤x<-$\frac{1}{3}$时,(*)化为:-2=2x-$\frac{3}{2}$,解得x=-$\frac{1}{4}$,舍去;
当$-\frac{1}{3}$≤x<0时,(*)化为:-1=2x-$\frac{3}{2}$,解得x=$\frac{1}{4}$,舍去;
当x∈$[\frac{n}{3},\frac{n+1}{3})$时(n∈N),(*)左边=n,右边<$\frac{4n-5}{6}$,而$\frac{4n-5}{6}$<n,因此无解.
综上可得:原方程的解为:x=-$\frac{5}{4}$或-$\frac{3}{4}$.
(3)x2-8[x]+7=0化为x2+7=8[x]≤8x,解得1≤x≤7.
化为[x]=$\frac{1}{8}({x}^{2}+7)$
当x∈[1,2)时,左边=1,右边≥1,此时有一解,x=1;当x∈[2,3)时,左边=2,右边<2,此时无解;
当x∈[3,4)时,左边=3,右边<3,此时无解;当x∈[4,5)时,左边=4,右边<4,此时无解;
当x∈[5,6)时,左边=5,右边∈$[4,\frac{43}{8})$,此时5=$\frac{1}{8}({x}^{2}+7)$,(x>0),解得x=$\sqrt{33}$,因此有一解$\sqrt{33}$;
当x∈[6,7)时,左边=6,右边∈$[\frac{43}{8},7)$,此时6=$\frac{1}{8}({x}^{2}+7)$,(x>0),解得x=$\sqrt{41}$,因此有一解$\sqrt{41}$;
当x=7时,左边=7,右边=7,因此有一解7.
综上可得:x=1,$\sqrt{33}$,$\sqrt{41}$,7.
(4)∵2[x]≤[2x]≤2[x]+1,
∴3[x]≤[x]+[2x]≤3[x]+1,
∵[x]+[2x]=18,
∴$\frac{17}{3}$≤[x]≤6,
∴6≤x<7,经过验证6.5≤x<7时不成立,
∴6≤x<6.5.
点评 本题考查了[x]的性质及其应用、解方程,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

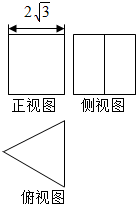 一个体积为12$\sqrt{3}$的正三棱柱(底面为正三角形,且侧棱垂直于底面的棱柱)的三视图如图所示,则该三棱柱的侧视图的面积为( )
一个体积为12$\sqrt{3}$的正三棱柱(底面为正三角形,且侧棱垂直于底面的棱柱)的三视图如图所示,则该三棱柱的侧视图的面积为( )| A. | 6$\sqrt{3}$ | B. | 8 | C. | 8$\sqrt{3}$ | D. | 12 |